Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 86
Hoerner [Referência 12, p. 3-25] especifica que o coeficiente de arrasto de uma bandeira de razão de aspecto de 2:1 é 0,11, com base na área planificada. A Universidade de Rhode Island tem um mastro de alumínio de 25 m de altura e 14 cm de diâmetro. Esse mastro serve para hastear as bandeiras nacional e estadual niveladas em conjunto. Se a tensão de fratura do alumínio for 210 MPa, que tamanho máximo de bandeira poderá ser usado a fim de evitar a ruptura do mastro durante furacões (121 km/h)? (Despreze o arrasto do mastro.)
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos um mastro de alumínio com comprimento e diâmetro , com duas bandeiras hasteadas: a dos EUA e a de Rhode Island, como mostra a figura abaixo:
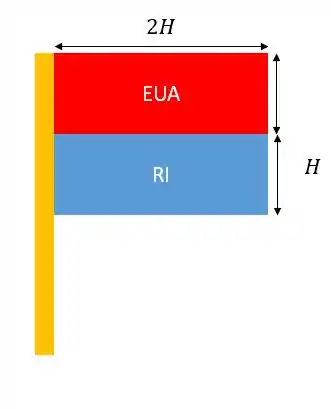
Como bem diz o enunciado da questão, as bandeiras têm uma razão de 2:1, e pra essa geometria seus coeficientes de arrasto são .
Pra uma fatura de e uma velocidade , a questão quer que a gente descubra o tamanho da bandeira. Faremos isso realizando um balanço de momento com as forças de arrasto para as duas bandeiras.
No próximo passo eu vou te mostrar como calcular a dimensão da bandeira, então vem comigo pra gente resolver esse problema juntos!
Passo 2
Nosso primeiro passo será calcular o momento agindo nesse sistema. Pra isso, vamos considerar uma fórmula pra tensão de fatura do alumínio:
Sendo o raio da barra e o momento de fratura.
Calculando , teremos:
Passo 3
Agora, iremos encontrar expressões pras forças de arrasto das duas bandeiras, e , que são iguais.
Faremos:
Sendo: a massa específica do ar e a área das bandeiras onde ocorre o escoamento.
Sendo assim, vamos ficar com:
Passo 4
Por fim, pra resolver a questão, devemos fazer um balanço de momento com relação à base do mastro.
Vamos entender que a linha de aplicação da força de arrasto em cada bandeira é diferente, por causa de sua posição no mastro.
O da bandeira dos EUA, por exemplo, está localizada da base do mastro, enquanto o da bandeira de Rhode Island econtra-se a da base do mastro.
Assim, o momento de fratura pode ser dado por:
Substituindo os valores que conhecemos:
Resolvendo essa equação cúbica pra , teremos:
Portanto, as dimensões das bandeiras são .
Pronto, matamos a questão juntos!
Resposta
As dimensões das bandeiras ideais par evitar a ruptura do mastro são