Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 39
Um avião foi projetado para cruzar a um número de Mach a , onde a temperatura atmosférica é de . Determine a temperatura de estagnação sobre a borda de ataque da asa.
Passo 1
O problema quer saber quanto vale a temperatura de estagnação do ar que está a , quando ele entra em contato com a asa de um avião.
A figura abaixo mostra os dados que temos para calcular .
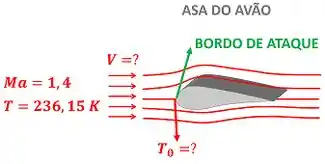
onde é o número de Mach do ar, é a temperatura do ar e é a velocidade do ar.
Para achar a temperatura de estagnação do ar, temos que encontrar antes a velocidade do ar.
Por isso, acharemos no próximo passo.
Passo 2
Para calcular a velocidade do ar, precisamos usar a equação do número de Mach (equação 12-12 do livro).
onde é a velocidade do som no ar.
A equação acima mostra que precisamos encontrar o valor da velocidade do som no ar para calcular .
A equação de para um gás ideal (o ar pode ser considerado um gás ideal) é a equação 12-11 do livro.
onde é a razão de calores específicos (no caso do ar, vale ) e é a constante do gás (no caso do ar ).
Substituindo essa fórmula na equação de , achamos:
Passo 3
Com os valores de velocidade calculados, podemos calcular a temperatura de estagnação do ar a partir da equação 12-4 do livro.
onde é o calor específico a pressão constante (no caso do ar, ).