Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas - Ex. 3
Um avião tem um comprimento de corda de L = 1,2 m e voa a Mach 0,7 na atmosfera padrão. Se seu número de Reynolds, com base no comprimento da corda, for de , a qual altitude ele está voando?
Passo 1
E aí, galeraaa!! Tranquilidade? Esse exercício aqui vamos precisar do auxílio da tabela A-6 que tem essa carinha aqui ó!!
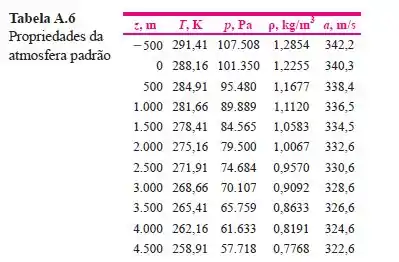
Note que a tabela já dá pra gente as alturas (z,m) de acordo com outros parâmetros. Então vamos primeiro supor que a temperatura seja de , na tabela você vai observar a seguinte linha!!
Passo 2
A partir da tabela supondo a temperatura de 230K, temos que aproximadamente!
O número de Mach é uma relação de ! O enunciado nos diz que seu valor é de 0,7!! OPAAAAAA, conseguimos então calcular nossa velocidade U, pois...
Com base na nossa temperatura tomamos das tabelas de propriedades físicas do ar do livro, então podemos agora estimar nosso valor de densidade que é o próximo parâmetro da tabela que vamos calcular!
Como fazer isso?
Com esse valor, se olharmos na tabela, ele dará pra gente um valor de altura de aproximadamente 9500 m (Dá uma olhadinha lá pra você conferir)!
Passo 3
Mas beleza, você consegue perceber que esse processo é iterativo? Porque eu tive que CHUTAR uma temperatura pra chegar até um valor de altitude. Então, agora como seria o processo?
Bem, com essa nova altitude calculada, você iria na tabela A-6, procuraria qual é a temperatura referente a essa altitude, obteria um novo valor de a, por consequência um novo valor de U, para encontrar um novo valor de densidade e por fim um novo valor de altitude. Esse processo deve ser feito até que o valor da densidade ou altura esteja convergindo!
Bem, você pode fazer esse processo aí no seu software de preferência. Eu fiz aqui e convergiu quando , ou seja