Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 77
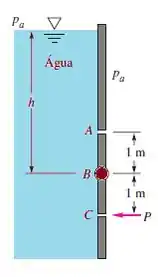
A comporta circular ABC na figura abaixo tem um raio de 1 m e é articulada em B. Calcule a força P exatamente suficiente para impedir que a comporta se abra quando h = 8 m. Despreze a pressão atmosférica.
Passo 1
A força hidrostática que atua no ponto B é dado por:
Passo 2
Mas sabemos que essa força atuará um pouquinho mais abaixo dessa posição B, uma vez que seu centro de pressão é mais embaixo. Então precisamos calcular esse centro de pressão:
Passo 3
A soma dos momentos que atuam em B deve ser igual a zero, certo?
Resposta
Exercícios de Livros Relacionados
A água de um reservatório com 25m de profundidade mantida no seu interior por uma parede com 150m de largura cuja seção transversal é um triângulo equilátero, como mostra a Figura P3-123. Determine (a
Um tubo em U contém água no braço direito e outro líquido no braço esquerdo. Observa-se que, quando o tubo em U gira a 30r p m em torno do eixo que está a 15c m do braço direito e 5c m do braço esquer
Um cilindro vertical com 1m de diâmetro e 2m de altura preenchido completamente com gasolina, cuja densidade é de740k g / m 3 . O tanque agora é posto a rodar em torno do seu eixo vertical a uma taxa
Repita o problema 3-106 para uma leitura de pressão manométrica de 240 k P a .
Um dispositivo de cilindro e pistão sem atrito e vertical contém um gás a 500k P a . A pressão atmosférica externa é de 100k P a e área do pistão é de 30c m 2 . Determine a massa do pistão.