Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 101

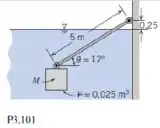
Um bloco de volume 0,025 m3 está imerso na água, conforme mostrado. Um tirante de seção circular de 5 m de comprimento e 20 cm2 de seção transversal está preso ao bloco assim como à parede. Se a massa do tirante é 1,25 kg e o tirante faz um ângulo de 12° com a horizontal, qual será a massa do bloco?

Passo 1

Neste problema temos a geometria de um bloco e um tirante, em que devemos encontrar a massa do bloco de acordo com o ângulo atribuído. Para isso devemos supor que a agua é estática e incompressível.

Usaremos algumas equações básicas para a resolução:

F = ρ g V d

∑ M d o b r a d i ç a = 0

De acordo com o diagrama abaixo, podemos analisar as forças:

∑ M d o b r a d i ç a = 0

Vamos chamar de F B H a força de flutuabilidade da haste e F B B a força de flutuabilidade do bloco, logo,

W B - F B B × L cos ⁡ θ + F B H × L + c 2 × cos ⁡ θ + W H × L 2 × cos ⁡ θ = 0

Sendo que F B H = ρ g L - c A , W R = M R g , F B B = ρ g V B e W B = M B g . Assim, podemos substituir na equação:

M B - ρ V B × L + ρ g A L - c × L + c 2 + M R × L 2 = 0

Passo 2

A equação que formamos no Passo 1, podemos isolar em relação a M B :

M B = ρ A 2 L L 2 - c 2 + ρ V B - M R 2

Como o comprimento é dado por: c = a sin ⁡ θ   :

M B = ρ A 2 L L 2 - a sin ⁡ θ   2 + ρ V B - M R 2

Agora é só substituir os dados:

M B = 1000 k g m 3 × 0,002   m 2 2 × 5 5 2 - 0,25 sin ⁡ 12 °   2 + 1000 × 0,025   m 3 - 1,25   k g 2

M B = 29,1   k g

Prontinho!!

Resposta

M B = 29,1   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma esfera de raio 25m m , feita de material de densidade específica S G=0,95 , está submersa em um tanque contendo água. A esfera é colocada sobre um furo de raio 1,88m m , no fundo do tanque. Quando
O balonismo a ar quente é um esporte popular. De acordo com um artigo recente, “os volumes de ar quente devem ser grandes porque o ar aquecido a 65 ° C acima da temperatura ambiente levanta apenas 0,2
O perfil da seção reta de uma canoa é modelado pela curva y = a x 2 , em que a = 3,89 m–1 e as coordenadas são medidas em pés. Suponha que a largura da canoa tenha valor constante w = 0,6 m em todo o
Quantifique o experimento realizado por Arquimedes para identificar o material da coroa do Rei Hiero. Suponha que você possa medir o peso da coroa do rei no ar, W a , e também o peso na água, W w . Ex
Se a massa M no Problema 3.101 for liberada do tirante, quanto do tirante permanecerá submerso na nova condição de equilíbrio? Qual será a força mínima para cima necessária para levantar a extremidade