Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 123

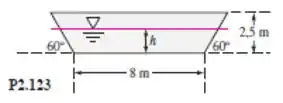
Uma barcaça tem a forma trapezoidal, mostrada na Figura P2.123, e 22   m de comprimento normal ao papel. Se o peso total da barcaça e sua carga for de 350 toneladas, qual é o calado H da barcaça quando estiver flutuando na água do mar?

Passo 1

Fala galera!! Tudo Certo?

Queremos nessa questão encontrar a altura h que está submersa. Para isso, podemos usar a ideia de que as forças que atuam na barcaça a mantém em equilíbrio, ou seja, a soma das forças é igual a zero.

Passo 2

Vamos supor que b é a largura no fundo, B é a largura na interface entre a água e o ar e L é o comprimento da barcaça, e seja γ o peso específico da água do mar. Assim, o volume de água do mar deslocado pode ser dado pela seguinte equação:

V = B + b   h L 2

A largura na interface, podemos obter por relação trigonométrica, ou seja:

B = 2 h tan ⁡ 60 + b

B = 2 h 3 + b

Passo 3

Podemos considerar P o peso da barcaça junto com sua carga 350 000   k g . Então, no equilíbrio temos o seguinte:

γ á g u a   d o   m a r V = P g

γ á g u a   d o   m a r B + b h L 2 = P g

γ á g u a   d o   m a r 2 h 3 + b + b h L 2 = P g

γ á g u a   d o   m a r 2 h 3 + 2 b h L 2 = P g

γ á g u a   d o   m a r h 3 + b h L = P g

Como o peso específico é a multiplicação a densidade pela gravidade:

ρ á g u a   d o   m a r g h 3 + b h L = P g

ρ á g u a   d o   m a r h 3 + b h L = P

Podemos obter a densidade da água do mar na Tabela A.3. Assim temos que:

ρ á g u a   d o   m a r = 1.025

Substituindo os dados fornecidos na equação encontrada, vamos ter:

1025 ⋅ h 3 + 8   h ⋅ 22 = 350 000

h 2 3 + 8 h = 15,52

h 2 + 13,85 h = 26,88

h 2 + 13,85 h - 26,88 = 0

Passo 4

Vem comigo que agora ficou mais fácil!!

Podemos usar a formula de Bhaskara para encontrar o valor de h . Assim temos:

h = - 13,85 ± 13,85 2 - 4 ⋅ 1 ⋅ - 26,88 2 ⋅ 1

h = - 13,85 ± 17,3 2

Como estamos interessados no valor positivo, temos que:

h = 1,72   m

Logo, a altura h que está submersa é 1,72   m .

Resposta

h = 1,72   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um corpo flutuante será estável quando:O seu centro de gravidade estiver acima de seu centro de empuxo;O centro de empuxo estiver abaixo da linha d’água;O centro de empuxo estiver acima do seu metacen
A 12-fl-oz glass, of 3-in diameter, partly full of water, isattached to the edge of an 8-ft-diameter merry-go-round,which is rotated at 12 r/min. How full can the glass bebefore water spills? Hint: As
A uniform cylindrical white oak log, ρ = 710 kg/m3, floatslengthwise in fresh water at 208C. Its diameter is 24 inches.What height of the log is visible above the surface?
A barge is 15 ft wide and 40 ft long and fl oats with a draftof 4 ft. It is piled so high with gravel that its center of gravity is 3 ft above the waterline. Is it stable?
A balloon weighing 3.5 lbf is 6 ft in diameter. It is filledwith hydrogen at 18 lbf/in2 absolute and 608F and isreleased. At what altitude in the U.S. standard atmospherewill this balloon be neutrally