Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 85
Calcule os componentes horizontal e vertical da força hidrostática no painel de um quarto de círculo no fundo do tanque de água da Figura P2.85.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 2.6 do livro, chamada “Forças sobre superfícies curvas”.
Pra entender a questão, dá uma olhada na figura do enunciado. Temos um painel de um quarto de círculo de de raio no fundo de um tanque de de altura e de largura.
A questão quer da gente as componentes horizontal e vertical da força hidrostática aplicada no painel de quarto de círculo, como mostra a imagem abaixo:
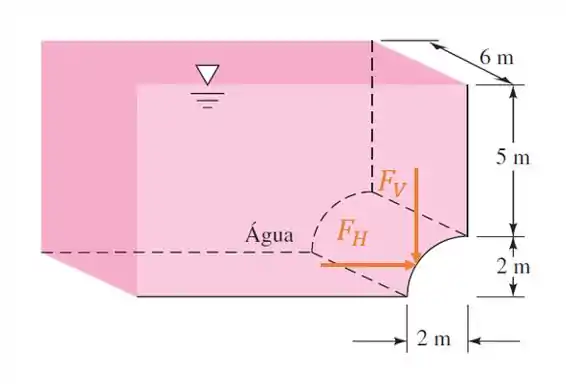
Nos próximos passos, nós vamos aprender juntos a calcular essas duas componentes. Vem comigo!
Passo 2
Primeiro, vamos calcular a componente horizontal . Para isso, devemos imaginar uma projeção em um ângulo de 90° com relação à direção dessa força, como na figura abaixo:
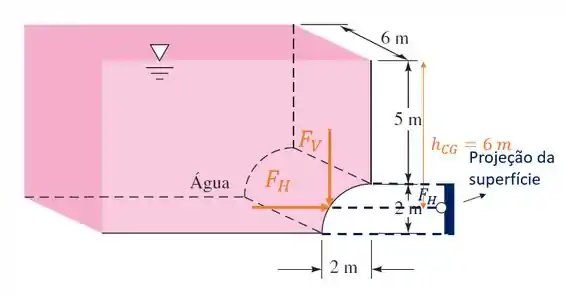
Observe que essa projeção é na verdade um retângulo, de base e altura . Sabendo disso, podemos definir a equação para calcular a componente vertical da força hidrostática:
Sendo: o peso específico, que para água à temperatura ambiente é 9790 ; a distância do centro de massa com relação à superfície livre; e a área do retângulo projetado.
Observem pela figura que vai até metade do raio do quarto de círculo, portanto . Portanto, a componente horizontal de força é igual a:
Passo 3
Pra finalizar a questão, vamos agora calcular o valor da componente vertical .
Pra saber como fazer esse cálculo, vamo olhar as imagens que já vimos nessa resolução, ou mesmo a própria figura esquemática do problema.
Você consegue perceber que o quarto de círculo se comporta como uma “parte retirada” do tanque, e que se ela não existisse teríamos um retângulo com de comprimento e de altura no exato lugar onde fica o quarto de círculo?
Pois bem, pra calcular a componente vertical da força hidrostática, devemos considerar o peso que a água teria se essa pequena área do tanque fosse completamente retangular, além do peso da água no próprio quarto de círculo.
A diferença entre esses dois pesos será o valor de :
Sendo o volume do retângulo e o volume do quarto de círculo
Calculando, temos:
Pronto, matamos o problema juntos!
Resposta
As componentes vertical e horizontal da força hidrostática são, respectivamente, e .