Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 131

A barge is 15 ft wide and 40 ft long and fl oats with a draft

of 4 ft. It is piled so high with gravel that its center of gravity is 3 ft above the waterline. Is it stable?

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Desenhando o diagrama mostrando o nível da água

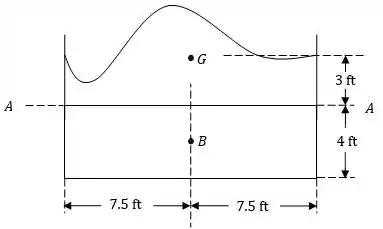
Passo 2

Calcule a distância entre o metacentro e a linha de água.

M A   = I o v sub  - B A   = b ( 2 L ) 3 / 12 2 L b H - H 2   = 8 b L 3 / 12 2 L b H - H 2   = L 2 3 H - H 2

Aqui, M é o metacentro, B é o centro da flutuabilidade, I o é o momento de inércia da área da linha de água, A é a linha de água, v sub  é o volume do corpo submerso, b é a largura da barcaça, L é a metade do comprimento da barcaça, H é a altura da barcaça e G é o centro de gravidade.

M A   = 7.5 2 3 × 4 - 4 2   = 2.69 f t

Passo 3

Calcule a distância entre o metacentro e o centro de gravidade da barcaça.

M G = M A - G

Aqui, M A é a distância entre o metacentro e a linha de água, e é a distância entre o G centro de gravidade da barcaça e a linha de água.

M G   = 2.69 - 3   = - 0.31 f t < 0

Portanto, a barcaça é instável, pois o valor de M G é negativo.

Resposta

Instável

Exercícios de Livros Relacionados

Um bloco uniforme de aço ( d = 7,85 ) “flutuará” em uma interface mercúrio-água, como mostra a Figura P2.122. Qual é a razão entre as distâncias a e b para essa condição?
A barra uniforme da Figura P2.121, de tamanho L por h por b e com o peso específico γ b , flutua exatamente em sua diagonal quando uma esfera uniforme pesada é presa ao canto esquerdo, como mostra a f
Considere um cone circular reto uniforme de densidade d1 , flutuando com seu vértice para baixo na água ( d = 1 ) . O raio da base é R e a altura do cone é H . Calcule e coloque em gráfico a estabilid
Ao flutuar em água ( d = 1,0 ) , um corpo triangular equilateral ( d = 0,9 ) pode assumir uma das duas posições mostradas na Figura P2.134. Qual é a posição mais estável? Considere que a largura seja
Considere um cilindro circular reto homogêneo de comprimento L , raio R e densidade d , flutuando em água ( d = 1 ) . Mostre que o corpo será estável com seu eixo vertical se R L2 d 1 - d 1 / 2