Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 82 b
Uma parede composta é feita com duas grandes placas separadas por folhas de isolamento refratário, como mostrado na figura. No processo de instalação, as folhas de espessura L = 50 mm e condutividade térmica k = 0,05 W/(m · K), são separadas em intervalos de 1 m por espaços de largura w = 10 mm. As placas quente e fria têm temperaturas e emissividades T1 = 400°C, ε1 = 0,85 e T2 = 35°C, ε2 = 0,5, respectivamente. Suponha que as placas e o isolante sejam superfícies difusas e cinzas.
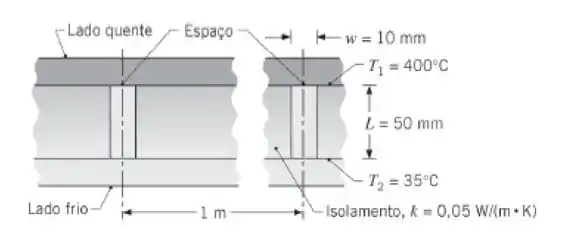
- Reconhecendo que os espaços estão localizados com um espaçamento de 1 m, determine qual fração da perda térmica total através da parede composta é devido à transferência por radiação através dos espaços do isolamento.
Passo 1
Vamos lá!!! Agora queremos saber qual é a porcentagem da perda de calor por radiação! Isso quer dizer que a gente vai ter que calcular a perda por condução!
A perda por condução vai acontecer de duas formas! A primeira é através do isolamento e a segunda é através do ar, a perda total é:
Passo 2
O enunciado da e pelo ar. Não temos mas esse valor é tabelado, !
Lembrando que tem uma folha de isolamento a cada e entre elas existe vazio, então para calcular :
E para calcular :
Substituindo:
Isolando os termos comuns:
Substituindo:
Calculando:
Passo 3
Agora a gente pode calcular o percentual da perda por radiação!!
Lembrando da letra :
Substituindo:
Ou: