Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 53
13.53 Um condutor elétrico muito longo, com 10 mm de diâmetro, está posicionado concentricamente no interior de um tubo cilíndrico resfriado, com 50 mm de diâmetro, cuja superfície é difusa e cinza com uma emissividade de 0,9 e está a temperatura de 27°C. O condutor elétrico tem uma superfície difusa e cinza com uma emissividade de 0,6 e está
dissipando 6,0 W por metro de comprimento. Considerando que há vácuo no espaço entre as duas superfícies, calcule a temperatura na superfície do condutor.
Passo 1
Vamos lá!! Antes de tudo, vamos desenhar um esqueminha do que ta acontecendo e já aproveitar pra converter os dados pro , vamos transformar os diâmetros em raios também, assim fica mais simples!
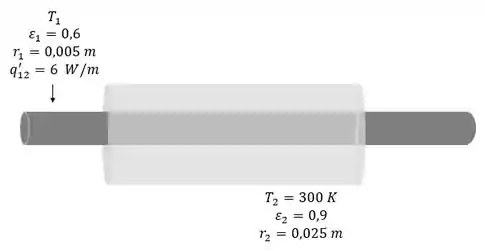
Agora que conseguimos visualizar o que ta acontecendo, vamos procurar a temperatura do condutor , lembrando que entre o condutor e o tubo resfriado há vácuo!
O que temos aqui são dois cilindros concêntricos, longos que estão deitados, certo?!
Então vamos usar a equação :
Passo 2
O enunciado nos da a informação do calor disspado por unidade de comprimento, então:
pode ser calculada:
Substituindo:
Podemos cortar e isolar ,!
Sabendo que , temos todas as informações, menos , podemos então substituir:
Calculando:
O enunciado da a temperatura em , então vamos dar a resposta em :
Ficamos com:
Uhuuuul!!