Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 40
Considere as superfícies negras inclinadas ( e ), muito longas,mantidas nas temperaturas uniformes de e
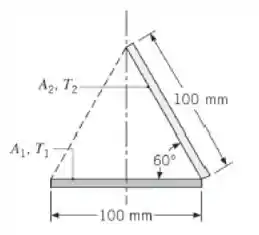
Determine a troca de radiação líquida entre as superfícies por unidade de comprimento das superfícies. Considere a configuração quando uma superfície negra (), cuja superfície posterior é isolada termicamente, está posicionada ao longo da linha tracejada mostrada na figura. Calcule a transferência de radiação líquida para a superfície , por unidade de comprimento da superfície, e determine a temperatura da superfície isolada .
Passo 1
Vamos lá!! Temos duas superfícies negras que dividem uma aresta em comum, formando um ângulo de e a primeira coisa que queremos é descobrir a troca de radiação líquida entre e por unidade de comprimento!
O problema nos fornece um desenho:
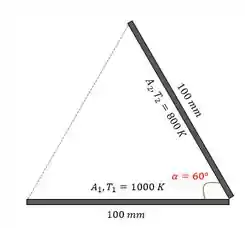
Para calcular a taxa de radiação entre as duas superfícies , temos:
Passo 2
Antes de qualquer coisa temos que conhecer o fator de forma, .
Sempre que a gente tiver em uma situação bidimensional , com de placas planas inclinadas de mesma largura que compartilham uma aresta, calculamos o fator de forma assim:
Com :
E por fim, o problema quer a taxa de radiação por unidade de comprimento, :
Substituindo, temos:
O problema é que a gente não conhece o comprimento, nem a área das placas, mas:
A largura a gente conhece!! Sabendo que , podemos calcular :
Calculando:
Passo 3
Agora gente tem uma segunda situação:
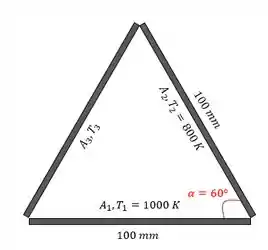
Agora estamos trabalhando com cavidade fechada e queremos descobrir !
Se a gente calcular , temos que considerar a troca de radiação das superfícies e :
Observando a imagem percebemos que:
Então:
Sabendo que a superfície é isolada, , então:
Podemos escrever:
Cortando os termos em comum:
Isolando :
Substituindo:
Calculando:
Passo 4
E pra terminar só falta calcularmos :
Como:
Podemos colocar alguns termos em evidência:
Substituindo:
Calculando:
Uhuuul!!