Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 124
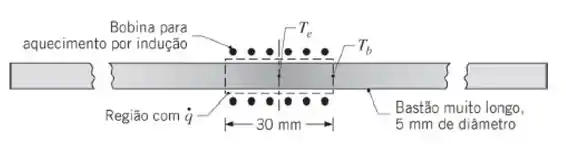
Um bastão muito longo, com 5 mm de diâmetro e condutividade térmica uniforme , é submetido a um processo de tratamento térmico. Sua porção central, com 30 mm de comprimento, está envolta por uma bobina de aquecimento por indução, havendo então, nesta porção, uma geração de calor volumétrica e uniforme de . Nas porções não aquecidas do bastão, continuações das duas extremidades da porção aquecida, há convecção com o ar a uma temperatura com . Suponha que não haja convecção na superfície do bastão no interior da bobina.
- Calcule a temperatura do bastão no ponto central da porção aquecida coberta pela bobina, no regime estacionário.
- Calcule a temperatura do bastão na extremidade da porção aquecida, no regime estacionário.
Passo 1
E aí? Como vocês estão ??
Espero que animadíssimos ein ...
Na letra (a) nós queremos achar a temperatura do bastão no ponto central da porção aquecida coberta pela bobina, ok?
Vimos no capítulo e até mesmo na questão anterior que quando estamos gerando energia teremos uma transferência de calor unidimensional e uniforme.
Usando a distribuição da temperatura para estes casos, dado pelo livro laaaa na Equação 3.47:
Se considerarmos este ponto central como sendo :
Infelizmente nós não temos nada sobre então vamos guardar esta informação e pular pra letra (b)!!
Passo 2
Nós sabemos que o calor gerado é o mesmo que passa por toda a aleta, certo?
Se considerarmos que o bastão se comporta como aleta infinita, podemos olhar na Tabela 3.4:
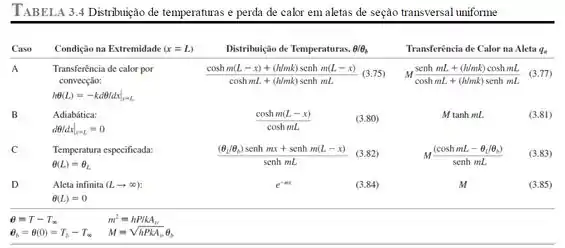
Sendo assim:
Substituindo
A taxa de transferência também pode ser escrita como:
Substituindo:
Passo 3
Na letra (c) nós temos que:
Calculando com ajuda do Passo 2:
Substituindo:
Em graus Celsius:
Agora podemos achar usando a fórmula do Passo 1:
Em graus Celsius:
Já obtemos os valores, certo?
Então finalizamos a letra (a) e (b) !!
Resposta
- ;