Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 122
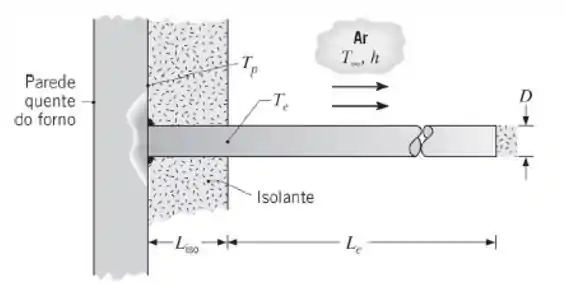
Um bastão com diâmetro D = 25 mm e condutividade térmica se estende perpendicularmente da parede externa de um forno, que está a , e está coberto parcialmente por um isolante com espessura . O bastão está soldado à parede do forno e é utilizado para sustentação de cabos de instrumentação. A fim de evitar danos aos cabos, a temperatura na superfície exposta do bastão, , deve ser mantida abaixo de um limite operacional especificado de . A temperatura do ar ambiente é e o coeficiente de transferência de calor por convecção é igual a .
- Desenvolva uma expressão para a temperatura da superfície exposta em função dos parâmetros térmicos e geométricos especificados. O bastão possui um comprimento exposto e a sua extremidade é isolada.
- Irá um bastão com atender ao limite de operação especificado? Se não, quais parâmetros de projeto você mudaria? Considere o uso de outro material, o aumento da espessura do isolante e o aumento do comprimento do bastão. Analise também como você poderia fazer a fixação da base do bastão à parede do forno a fim de reduzir .
Passo 1
Vamos para mais umaa ??
Então vamos fazer um desenho das resistências do que está acontecendo aqui, ok?
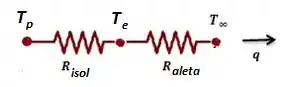
Se o calor é dado pela variação da temperatura sobre a resistência total:
Reorganizando:
Aaaaaa já achamos !!
A letra (a) foi tranquilex !!
Passo 2
Na letra (b) nós queremos saber se um bastão com atende ao limite de operação especificado,
Vamos ver nossos dados?
Se lembram como calculamos a resistência?
E da aleta basta olharmos a Tabela 3.4, ok?
Como:
Calculando as resistências:
Agora é só substituir na fórmula do Passo 1:
Sendo assim, não atenderá às especificações, certo? Já que .
Então nós devemos diminuir o valor da razão , certo?
Mas como? Se olharmos atentamente para as fórmulas dadas nós podemos perceber que existem cinco opções distintas, bora ver?
- Aumentar significativamente o comprimento , já que aumentando de maneira significante vamos aumentar a tanh e diminuir a resistência da aleta;
- Se diminuirmos a condutividade térmica do material vamos diminuir as duas resistências. Se igualarmos vamos obter , ou seja, podemos usar uma aleta de aço inoxidável.
- Se aumentarmos a espessura do isolamento nós teremos uma resistência de isolamento maior, aumentando o denominador da nossa razão nós a diminuímos, certo?
- Também poderíamos introduzir uma resistência de contato entre a aleta e a parede, que nos daria o mesmo princípio da solução (3).
- Também podemos aumentar o coeficiente de convecção, pois isso diminuiria a resistência da aleta.