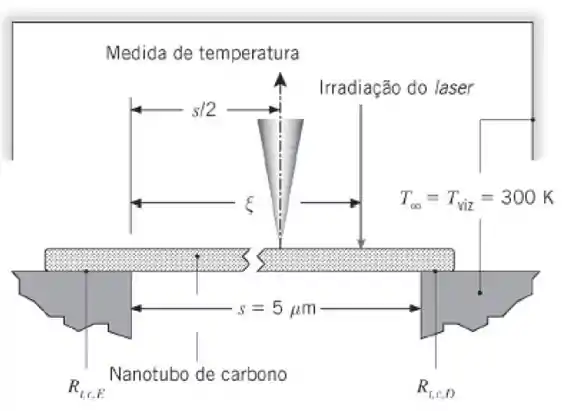
Um nanotubo de carbono está suspenso atravessando uma vala de largura s = 5 mm que separa duas ilhas, cada uma a . Um feixe laser irradia o nanotubo, a uma distância ξ da ilha esquerda, fornecendo q = 10 μW de energia para o nanotubo. A temperatura do nanotubo é medida no centro da vala utilizando um sensor pontual. A temperatura do nanotubo medida é para e para . Determine as duas resistências de contato, e nas extremidades esquerda e direita do nanotubo, respectivamente. O experimento é realizado em uma câmara de vácuo com . A condutividade térmica e o diâmetro do nanotubo são e D = 14 nm, respectivamente.
Passo 1
Vamos para mais umaa ??
Então vamos fazer um desenho das resistências do que está acontecendo aqui, ok?
O laser pode estar localizado a duas distâncias diferentes, e , o que faz o laser estar próximo da ilha da direita ou da esquerda, concordam?
Beleza, se sabemos disso podemos desenhar para o primeiro caso e depois ir seguindo:
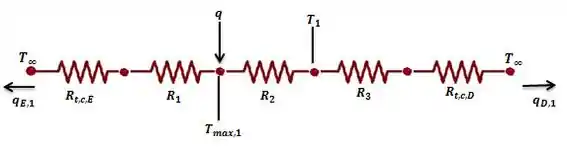
Beleza, nós desenhamos várias resistências porque a condução do calor depende da distância, certo?
A quantidade de calor total vai se distribuir no calor que caminha para esquerda e para direita:
Agora nós vamos ter que achar cada termo separadamente, ok?
Se o calor é dado pela variação da temperatura sobre a resistência total:
Agora nós vamos ver como se calcula cada resistência, lembrando que ela é dada pela distância dividida pela condutividade térmica e a área !!
Se já lembramos disso é só calcular:
Vamos ver nossos dados?
Substituindo tudo na fórmula do calor:
Podemos usar mais uma relação para
Passo 2
Agora, quando :
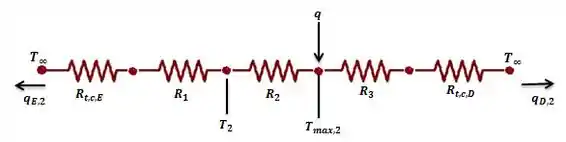
A quantidade de calor total vai se distribuir no calor que caminha para esquerda e para direita:
Agora nós vamos ter que achar cada termo separadamente, ok?
Se o calor é dado pela variação da temperatura sobre a resistência total:
Se já lembramos disso é só calcular:
Vamos ver nossos dados?
Substituindo tudo na fórmula do calor:
Agora nós vamos fazer o mesmo procedimento que no passo 1 e obter mais duas equações, certo?
Quando resolvemos estas quatro equações simultaneamente nós teremos os seguintes resultados:
Ufaaaa !! Pesada, não foi?