Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 149
Uma batata pode ser considerada como uma esfera sólida de 5,7 cm de diâmetro com as propriedades . Doze dessas batatas inicialmente a 25°C devem ser cozidas colocando-as em um forno mantido a 250°C, com um coeficiente de transferência de calor de . A quantidade de calor transferido para as batatas até o centro atinge a temperatura de 90°C é:
a) 1012 kJ;
b) 1366 kJ;
c) 1788 kJ;
d) 2046 kJ;
e) 3270 kJ.
Passo 1
Vamoo que vamooo!!
Primeiro, nós queremos achar o que?
O calor transferido para as batatas para que o centro atinja 90°C, certo?
Para isso vamos usar a equação:
Vamos começar achando o primeiro termo, Se lembram como?
Se:
Então:
Para achar o termo nós precisamos, antes de qualquer coisa, do número de Biot:
Sabemos que:
Agora é só calcular o Biot:
Passo 2
Olhando a Tabela:
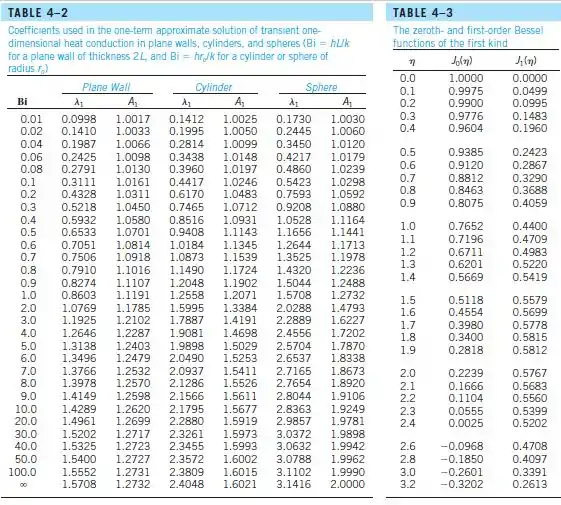
Como não temos o valor de Biot nós precisamos interpolar:
Usando os dados para uma esfera:
Substituindo:
Já temos dois dados para calcular o calor, agora nós só precisamos achar o calor máximo!
Vamos ver a fórmula?
Se:
Agora só precisamos da massa, mas isso é moleza!! Vamos usar a densidade:
Por ser uma esfera:
Como:
Então:
Achando o calor máximo:
Passo 3
Se temos todos os dados só nos resta colocar na fórmula do Passo 1:
Sendo assim, para que a temperatura do centro das 12 batatas atinja 90°C nós precisamos de
Aproximadamente, nossa resposta correta será a letra (b)!!
Grandinha, não ?
Mas acabamos !! :P