Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 137

Um homem é encontrado morto em um quarto a 12°C. A temperatura da superfície sobre sua cintura é de 23°C, e o coeficiente de transferência de calor é estimado em 9 W m 2 K . Tratando o corpo como um cilindro de 28 cm de diâmetro e 1,80 m de comprimento, estime quanto tempo se passou depois que ele morreu. Considere as propriedades do corpo como k = 0,62 W m K   e   α = 0 , 15 × 10 - 6 m 2 s e a temperatura inicial do corpo como 36°C.

Passo 1

Animados para continuar??

Espero que sim !!!!

Bom turminhaa, para achar a temperatura em um cilindro semi-infinito nós podemos usar a seguinte relação:

T - T α T i - T α = θ s e m i - i n f i n i t o ( x , t ) × θ c i l i n d r o ( r , t )

Para começar nós vamos considerar que o cilindro é infinitamente longo, então vamos começar avaliando o número de Biot:

B i = h r k

Sabemos que:

h = 9 W m 2 K

k = 0,62 W m K

r = d 2 = 0,28   m 2 = 0,14   m

Substituindo:

B i = 9 W m 2 K 0,14   m 0,62 W m K = 2,03

Olhando a Tabela:

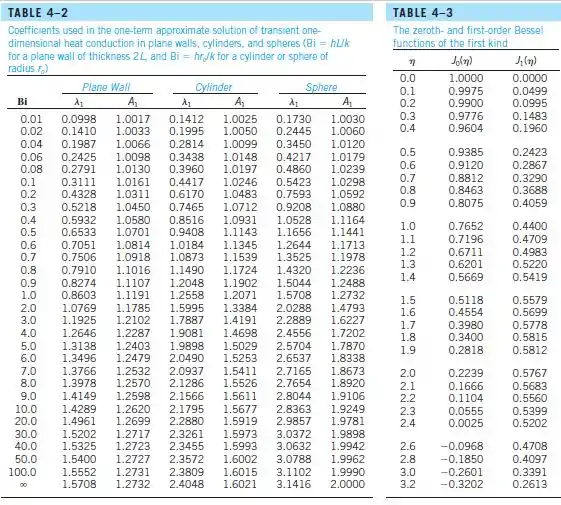
Como não temos o valor de Biot nós precisamos interpolar:

λ = λ B i 1 + B i - B i 1 λ   B i 2 - λ   B i 1 B i 2 - B i 1

A = A B i 1 + B i - B i 1 A   B i 2 - A   B i 1 B i 2 - B i 1

Usando:

B i 1 = 2,0 →   λ   B i 1 = 1,5995     e         A   B i 1 = 1,3384

B i 2 = 3,0 →   λ   B i 2 = 1,7887     e       A   B i 2 = 1 , 4191

Substituindo:

λ = 1,5995 + 2,03 - 2,0 1,7887 - 1,5995 3,0 - 2,0 = 1,6052

A = 1,3384 + 2,03 - 2,0 1,4191 - 1,3384 3,0 - 2,0 = 1,3408

Com isto nós somos capazes de achar mais um valor importante:

J 0 λ = J 0 ( λ B i 1 ) + λ - λ   B i 1 J 0 ( λ B i 2 ) - J 0 ( λ B i 1 ) λ   B i 2 - λ   B i 1

Usando:

  λ   B i 1 = 1,6 →   J 0 λ B i 1 = 0,4554

λ   B i 2 = 1,7 →   J 0 λ B i 2 = 0,3980

Substituindo:

J 0 λ = 0,4554 + 1,6052 - 1,6 0,3980 - 0,4554 1,7 - 1,6 = 0,4524

Agora que temos estes dados podemos calcular a temperatura adimensional para o cilindro usando a fórmula:

θ c i l i n d r o ( r , t ) = A e - λ 2 τ . J 0 ( λ )

Colocando nossos dados:

θ c i l i n d r o ( r , t ) = 1,3408 . e - ( 1,6052 ) 2 τ . ( 0,4524 )

θ c i l i n d r o ( r , t ) = 0,6066 . e - 2,5767 . τ

Do cilindro nós já achamos!! Agora vamos achar a temperatura para a parede, ok?

Passo 2

Novamente vamos calcular o número de Biot:

B i = h L c k

Sabemos que:

h = 9 W m 2 K

k = 0,62 W m K

L c = L 2 = 1 , 8   m 2 = 0 , 9   m

Substituindo:

B i = 9 W m 2 K 0 , 9   m 0,62 W m K = 1 3 , 06

Olhando a Tabela:

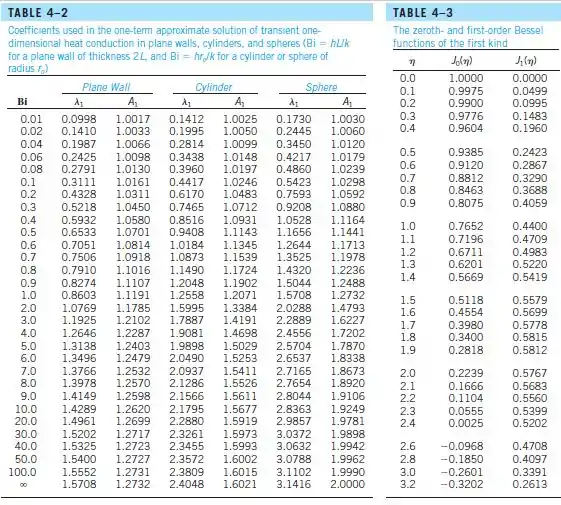
Como não temos o valor de Biot nós precisamos interpolar:

λ = λ B i 1 + B i - B i 1 λ   B i 2 - λ   B i 1 B i 2 - B i 1

A = A B i 1 + B i - B i 1 A   B i 2 - A   B i 1 B i 2 - B i 1

Usando:

B i 1 = 10 →   λ   B i 1 = 1 , 4289     e         A   B i 1 = 1 , 2620

B i 2 = 20 →   λ   B i 2 = 1 , 4961     e       A   B i 2 = 1 , 2699

Substituindo:

λ = 1,4289     + 13 , 0 6 - 1 0 , 0 1,4961 - 1,4289     20 - 1 0 = 1 , 4495

A = 1,2620 + 13,06 - 10,0 1,2699 - 1,2620 20 - 10 = 1 , 264

Agora que temos estes dados podemos calcular a temperatura adimensional para a parede usando a fórmula:

θ s e m i - i n f i n i t o ( x , t ) = A e - λ 2 τ

Colocando nossos dados:

θ s e m i - i n f i n i t o ( x , t ) = 1 , 264 . e - ( 1 , 4495 ) 2 τ

θ s e m i - i n f i n i t o ( x , t ) = 1,264 . e - 2 , 1009 . τ

Passo 3

Agora que nós temos as temperaturas adimensionais nós podemos fazer a temperatura combinada colocando o que nós achamos na fórmula do Passo 1:

T - T α T i - T α = 1,264 . e - 2,1009 . τ × 0,6066 . e - 2,5767 . τ

Vamos substituir o número de Fourier em função do tempo, que é o que queremos, certo?

τ = α t L c ²

Na fórmula:

T - T α T i - T α = 1,264 . e - 2,1009 . α t L c ² × 0,6066 . e - 2,5767 . α t L c ²

Se:

α = 0 , 15 × 10 - 6 m 2 s

L c = 0,9   m

T = 23 ° C

T α = 12 ° C

T i = 36 ° C

Então:

23 ° C - 12 ° C 36 ° C - 12 ° C = 1,264 . e - 2,1009 . 0 , 15 × 10 - 6 m 2 s t ( 0,9 m ) ² × 0,6066 . e - 2,5767 . 0 , 15 × 10 - 6 m 2 s t ( 0,9 m ) ²

0 , 46 = 0,762 . e - 2,011 × 10 - 5 s - 1 t

Aplicamos o ln:

t = 25098   s

Em horas:

t = 25098   s × 1   h 3600   s   = 6,97   h

Bem puxada !! Mas deu pra entender, não foi?

Resposta

6,97   h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma placa de espessura de 2,5 cm, um cilindro longo de diâmetro 2,5 cm e uma esfera de diâmetro 2,5 cm, todos inicialmente a 200 °C e todos feitos de bronze ( k=26W / m . ° Ceα=8,6 x 10 - 6
Grandes placas de um produto alimentar com 8 cm de espessura hermeticamente embaladas em papel fino são resfriados em uma câmara frigorífica mantida a 0 °C. O coeficiente de transferência de calor nas
Considere um bloco de motor de carro ( k=52W / m . Keα=1,7 x 10 - 5 m ² / s ² ). O motor pode ser considerado um bloco retangular cujos lados são 80, 40 e 40 cm. O motor está na temperatura de 150 °C
Considere um leito compactado de esferas, cada uma com diâmetro D = 2m m , a uma temperatura inicial T i = 95 ° C . Água fria a T w = 5 ° C é despejada no leito em t = 0 , produzindo um grande coefici
86 – Durante os meses de inverno frio, um escritório é parcialmente aquecido extraindo energia térmica armazenado no solo abaixo, usando uma bomba de calor. Durante o verão, o prédio é parcialmente re