Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 106
Deduza uma expressão para a razão da energia total transferida a partir da superfície isotérmica de uma esfera para o seu interior, , que seja válida para . Represente os seus resultados em termos do número de Fourier, .
Passo 1
Aqui nós temos uma esfera com temperatura constante da superfície. E queremos encontrar a expressão para em função de .
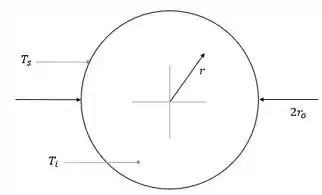
Passo 2
Para resolver essa questão nós vamos considerar que a condução é unidimensional e as propriedades são constantes. Da Tabela 5.2a. para temos:
Onde,
Substituindo a expressão por na primeira equação ficamos com:
Passo 3
Nós queremos uma expressão para . Então,
Assim, temos que:
Resposta
Exercícios de Livros Relacionados
Para permitir o cozimento de uma ampla gama de alimentos em fornos de micro-ondas, materiais de empacotamento metálicos e finos, que absorvem facilmente a energia das micro-ondas, foram desenvolvidos.
Um disco ótico regravável (DVD) é formado colocando-se um material de armazenamento composto binário, com 15n m de espessura, entre duas folhas de 1m m de policarbonato. Os dados são escritos no meio
Para permitir o cozimento de uma ampla gama de alimentos em fornos de micro-ondas, materiais de empacotamento metálicos e finos, que absorvem facilmente a energia das micro-ondas, foram desenvolvidos.
Considere um leito compactado de esferas, cada uma com diâmetro D = 2m m , a uma temperatura inicial T i = 95 ° C . Água fria a T w = 5 ° C é despejada no leito em t = 0 , produzindo um grande coefici
86 – Durante os meses de inverno frio, um escritório é parcialmente aquecido extraindo energia térmica armazenado no solo abaixo, usando uma bomba de calor. Durante o verão, o prédio é parcialmente re