Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 34

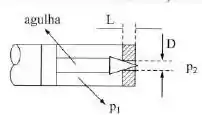
O bico injetor de um sistema de injeção eletrônica para motores é constituído de uma agulha que levanta, liberando um orifício que injeta o combustível devido a uma diferença de pressão Δ p entre a entrada e a saída. Sabe-se que a vazão em volume Q que escoa pelo orifício é função da viscosidade do fluido μ , do diâmetro do orifício D e de Δ p L . Adotando como base μ ,   Δ p L e D , sabendo-se que para um dado motor o orifício tem D = 0,5   m m , qual o diâmetro do orifício para outro motor que necessita de 20 % a mais de vazão de combustível, mantidas todas as outras variáveis?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para resolver este exercício vamos usar a análise dimensional para calcular o diâmetro do orifício.

A vazão volumétrica é dada por:

Q = L 3 T - 1

A viscosidade dinâmica será:

μ = F L - 2 T

A variação de pressão em relação ao comprimento é dada por:

∆ P L = F L = F L - 1

O diâmetro é uma unidade de comprimento, portanto:

D = L

Passo 2

Dadas as dimensões, podemos descrever os termos da equação como:

Q = μ x ∆ P L y D z

Substituindo, temos que:

L 3 T - 1 = F L - 2 T x F L - 1 y L z

Desenvolvendo, temos que:

L 3 T - 1 = F x + y L - 2 x - y + z T x

Igualando os expoentes dos dois lados, temos que:

x + y = 0

- 2 x - y + z = 3

x = - 1

Sendo assim, temos que:

y = 1

z = 2

Passo 3

Sendo assim, podemos dizer que:

1,2 Q 1 = Q 2

Como:

Q = v μ   D 2

Temos que:

1,2 D 1 2 = D 2 2

1,2 0,5 2 = D 2 2

Resolvendo, temos que:

D 2 = 0,548   m m

Resposta

D 2 = 0,548   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar uma expressão para o período de oscilação de um pêndulo simples, de comprimento l , que oscila com amplitude reduzida devido unicamente à ação da gravidade.
A força resultante F, exercida por um fluido sobre um perfil de asa de comprimento característico L, depende da massa específica ρ e da viscosidade dinâmica μ do fluido, da velocidade v do perfil em r
A velocidade v com que o fluido atravessa o vertedor triangular da figura é uma função da aceleração da gravidade g e da altura h da superfície livre do líquido em relação ao vértice do triãngulo. Det
A vazão Q de um líquido ideal que escoa para a atmosfera através de um orifício de bordo delgado, praticado na parede lateral de um reservatório, é função do diâmetro D do orifício, da massa específic
A pressão efetiva p, num ponto genérico de um líquido em repouso, é função da massa específica ρ , da aceleração da gravidade g e da profundidade do ponto h em relação à superfície livre do líquido. D