Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 6.Exercício - Ex. 10

A força resultante F, exercida por um fluido sobre um perfil de asa de comprimento característico L, depende da massa específica ρ e da viscosidade dinâmica μ do fluido, da velocidade v do perfil em relação ao fluido e do ângulo de ataque α . Determinar a função de adimensionais equivalente.

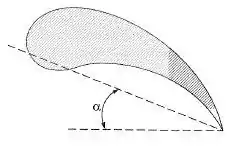
Passo 1

Nesse exercício, estamos interessados em analisar a força resultante F, que é função de:

F = f v , α , L , ρ , μ

O primeiro passo é identificar a função representativa, nesse caso, então, será:

f v , α , L , ρ , μ , F = 0

Agora vamos escrever a equação dimensional para cada uma das grandezas:

ρ = M L - 3 ; v = L T - 1 ; L = L ; μ = M L - 1 T - 1 ; F = M L T - 2 ;

α = M 0 L 0 T 0 = 1   ( j á   é   a d i m e n s i o n a l )

Agora vamos calcular o número de adimensionais independentes m = n - r , nesse caso temos:

n = 6   g r a n d e z a s   e n v o l v i d a s   n o   f e n ô m e n o

r = 3   n ú m e r o   d e   g r a n d e z a s   f u n d a m e n t a i s   d o   f e n ô m e n o

Sendo assim, temos:

m = 6 - 3 → m = 3   ( g r u p o s   d i m e n s i o n a i s )

Passo 2

Agora vamos construir os números adimensionais:

π 1 = ρ α 1 v α 2 L α 3 μ  

π 2 = ρ β 1 v β 2 L β 3 F

π 3 = ρ δ 1 v δ 2 L δ 3 α

Agora, substituindo cada uma das grandezas dimensionais nas equações, temos:

π 1 = ρ α 1 v α 2 L α 3 μ = M L - 3 α 1 L T - 1 α 2 L α 3 M L - 1 T - 1

Então, para que π 1 seja adimensional, temos:

α 1 + 1 = 0 → α 1 = - 1

- α 2 - 1 = 0 → α 2 = - 1

- 3 α 1 + α 2 + α 3 - 1 = 0 → - 3 - 1 + ( - 1 ) + α 3 - 1 = 0 → α 3 = - 1

Dessa forma, temos então:

π 1 = ρ - 1 v - 1 L - 1 μ → π 1 = μ ρ v L → R e = ρ v L μ R e y n o l d s

Agora, repetindo o processo para π 2 :

π 2 = ρ β 1 v β 2 L β 3 F = M L - 3 β 1 L T - 1 β 2 L β 3 M L T - 2

Então, para que π 2 seja adimensional, temos:

β 1 + 1 = 0 → β 1 = - 1

- β 2 - 2 = 0 → β 2 = - 2

- 3 β 1 + β 2 + β 3 + 1 = 0 → - 3 - 1 + - 2 + β 3 + 1 = 0 → β 3 = - 2

Dessa forma, temos então:

π 2 = ρ - 1 v - 2 L - 2 F → π 2 = F ρ v 2 L 2 → E u = F ρ v 2 L 2 E u l e r

Passo 3

Agora vamos encontrar π 3 :

π 3 = ρ δ 1 v δ 2 L δ 3 α = M L - 3 δ 1 L T - 1 δ 2 L δ 3 M 0 L 0 T 0

Então, para que π 3 seja adimensional, temos:

δ 1 + 0 = 0 → δ 1 = 0

- δ 2 + 0 = 0 → δ 2 = 0

- 3 δ 1 + δ 2 + δ 3 + 0 = 0 → - 3 0 + - 1 + δ 3 = 0 → δ 3 = 0

Dessa forma, temos então:

π 3 = ρ 0 v 0 L 0 α → π 3 = α

Sendo assim, a função de adimensionais será:

f π 1 , π 2 , π 3 = f ρ v L μ ; F ρ v 2 L 2 ; α

Resposta

f ρ v L μ ; F ρ v 2 L 2 ; α

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O torque, T , de uma máquina manual para polir automóvel é uma função da velocidade de rotação, ω , da força normal aplicada, F , da rugosidade superficial do automóvel, e , da viscosidade da pasta po
A função representativa de um certo fenômeno é f ρ ; μ ; v ; F ; c ; L = 0 . Onde c = velocidade do som e L é o comprimento característico qualquer. Como no laboratório os ensaios são realizados com b
O bico injetor de um sistema de injeção eletrônica para motores é constituído de uma agulha que levanta, liberando um orifício que injeta o combustível devido a uma diferença de pressão Δ p entre a en
Ondas de superfície livre começam a formar­se sobre uma película laminar de um líquido escoando para baixo sobre uma superfície inclinada sempre que o número de Reynolds, baseado na vazão mássica por
O projeto de automóveis está tendendo para a tração nas quatro rodas de modo a melhorar o desempenho e a segurança do veículo. Um veículo de tração total deve ter um diferencial especial para permitir