Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 6.Exercício - Ex. 6

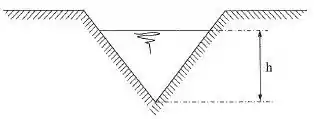
A velocidade v com que o fluido atravessa o vertedor triangular da figura é uma função da aceleração da gravidade g e da altura h da superfície livre do líquido em relação ao vértice do triãngulo. Determinar a expressão para a vazão.

Passo 1

O primeiro passo é identificar a função representativa, nesse caso, estamos analisando a velocidade, sabemos que a velocidade é função de:

v = f g , h

Então, a função representativa será

f g , h , v = 0

Agora vamos escrever a equação dimensional para cada uma das grandezas:

g = L T - 2 ; h = L ;   v = L T - 1

Agora vamos calcular o número de adimensionais independentes m = n - r , nesse caso temos:

n = 3   g r a n d e z a s   e n v o l v i d a s   n o   f e n ô m e n o

r = 2   n ú m e r o   d e   g r a n d e z a s   f u n d a m e n t a i s   d o   f e n ô m e n o

Sendo assim, temos:

m = 3 - 2 → m = 1   ( g r u p o s   d i m e n s i o n a i s )

Como temos m = 1 , então o grupo dimensional será uma constante C .

Passo 2

Agora vamos construir os números adimensionais:

π 1 = g α 1 h α 2 v

Agora, substituindo cada uma das grandezas dimensionais nas equações, temos:

π 1 = g α 1 h α 2 v = L T - 2 α 1 L α 2 L T - 1

Então, para que π 1 seja adimensional, temos:

- 2 α 1 - 1 = 0 → α 1 = - 1 2

α 1 + α 2 + 1 = 0 → α 2 = - 1 - - 1 2 → α 2 = - 1 2

Dessa forma, temos então:

π 1 = g - 1 2 h - 1 2 v → π 1 = v g h → v = π 1 g h

Passo 3

Agora, sabemos que a fórmula da vazão é dada por:

Q = v A

E, podemos escrever a área de um triângulo como:

A = b h 2

Sendo α o ângulo do vértice da base do vertedor da figura do enunciado, então podemos escrever:

tg ⁡ α 2 = b 2 h → b = 2 h tg ⁡ α 2

Substituindo essa expressão na equação para a área, temos:

A = 2 h t g α 2 h 2 → A = h 2 t g α 2

Agora, substituindo esse valor e o valor encontrado para v no passo 2, temos:

Q = v A = π 1 g h h 2 t g α 2

Como π 1 e t g ( α / 2 ) são constantes, sua multiplicação também é uma constante, então, a vazão será:

Q = C g h 5

Resposta

Q = C g h 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Microcomponentes eletrônicos (microchips) são suportados por uma fina película de ar sobre uma superfície horizontal durante um estágio do processo de fabricação. Os “chips” têm 11,7 mm de comprimento
O perfil de velocidade para escoamento completamente desenvolvido de tetracloreto de carbono a 15°C entre placas paralelas (espaçamento a = 1,25 mm), com a placa superior em movimento, é dado pela Eq.
Um inventor propõe fabricar um “cronômetro viscoso” colocando um cilindro pesado dentro de outro cilindro ligeiramente maior contendo um líquido viscoso, formando assim uma película anular delgada ent
Um mancal de deslizamento consiste de um eixo de diâmetro D = 35 mm e comprimento L = 50 mm (momento de inércia I = 0,125 kg · m2 ) instalado simetricamente em um invólucro estacionário de modo que a
A eficiência da bomba de arrasto viscoso da Fig. P8.39 é dada por η = 6 q 1 - 2 q 4 - 6 q em que q = Q/abRω é uma vazão adimensional (Q é a vazão volumétrica para o diferencial de pressão Δp, e b é a