Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 55

Um bloco de peso está sendo puxado sobre uma mesa por um outro peso , como mostra a Figura . Encontre uma fórmula algébrica para a velocidade constante do bloco se ele desliza sobre um filme de óleo de espessura e viscosidade . A área inferior do bloco está em contato com o óleo. Despreze o peso da corda e o atrito na polia. Considere um perfil linear de velocidade no filme de óleo.

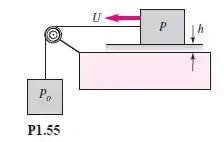
Passo 1

E aí, tudo bem? Bora matar essa questão rapidinho!

Olha nosso problema é MUUUUITO parecido com o problema e vamos resolver ele de maneira semelhante, só temos algumas alterações básicas!

A primeira que a força que puxa o bloco é a mesma força peso que atua no bloco em queda! E a segunda é que não tem ângulo de inclinação!

Vamos montar um esquema para ilustrar essa situação!

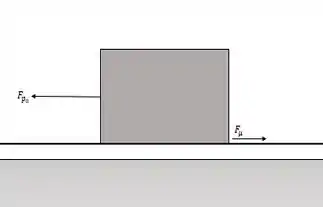
Passo 2

Agora pra matar essa questão vamos fazer um somatório de forças!

Isolando temos:

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

0 Considere o campo de escoamento V =a x t i+b j , em que a= 1 4 s - 2 e b=1 / 3m / s . As coordenadas são medidas em metros. Para a partícula que passa pelo ponto ( x ,y )=( 1 ,2 ) no instante t=0 ,

Considere o campo de velocidade do Problema 2.20. Trace a linha de emissão formada por partículas que passaram pelo ponto ( 1 ,1 ) durante o intervalo de tempo de t=0 a t=3s . Compare com as linhas de

Um escoamento é descrito pelo campo de velocidade = at + b , em que a=0,4m / 2 e b=2m / s . Em t=2s , quais são as coordenadas da partícula que passou pelo ponto (2, 1) em t = 0? Em t=3s , quais são a

Considere o campo de velocidades V → = a x î + b y ( 1+c t ) j ^ î , em que a = b = 2s - 1 e c = 0,4s - 1 . As coordenadas são medidas em metros. Para a partícula que passa pelo ponto ( x ,y ) =( 1 ,1

CConsidere o campo de escoamento dado na descrição euleriana pela expressão V → = a x î + b y t j ^ î , em que a = 0,2s - 1 , b = 0,04s - 2 e. e as coordenadas são medidas em metros. Deduza as funções