Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 5.Exercício - Ex. 14
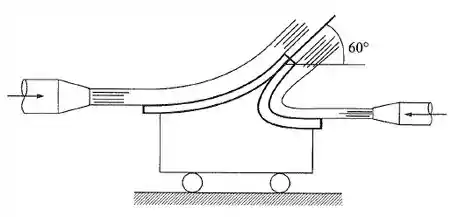
O bocal da esquerda tem uma área de 30 cm² e lança um jato com velocidade de 10 m/s contra a pá. O sistema está em equilíbrio. Qual é a vazão do segundo bocal e qual é a velocidade do jato se a área do bocal é 10 cm²? (O fluido é água com .)
Passo 1
Vamos começar o exercício analisando o bocal da esquerda e a força que o fluido aplica sobre o anteparo, a equação para a força exercida pelo fluido é dada por:
Vamos aplicar a equação na direção :
Como a vazão é constante e o diâmetro do jato também, então temos , e podemos escrever a vazão mássica do bocal da esquerda como:
Substituindo essa expressão na equação para a força, temos:
Passo 2
Agora vamos fazer a mesma análise, só que para o bocal da esquerda.
Vamos aplicar a equação na direção :
Como a vazão é constante e o diâmetro do jato também, então temos , e podemos escrever a vazão mássica do bocal da direita como:
Substituindo essa expressão na equação para a força, temos:
Passo 3
Como o enunciado nos disse que o sistema está em equilíbrio, então as forças da esquerda e da direita devem ser iguais, igualando as expressões encontradas, temos:
Substituindo os valores conhecidos, temos:
Agora podemos finalmente encontrar o valor da vazão volumétrica do bocal da direita: