Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 74
Um bocal de incêndio está conectado a uma mangueira de lona de 30 m de comprimento e 75 mm de diâmetro (com ). Água de um hidrante é fornecida a 345 kPa para uma bomba auxiliar na carroceria do carro de bombeiros. Nas condições de operação de projeto, a pressão na entrada do bocal é 690 kPa, e a perda de carga ao longo da mangueira é de 7,5 kPa/m para o comprimento. Calcule a vazão de projeto e a máxima velocidade na saída do bocal. Selecione uma bomba apropriada para esta aplicação, determine sua eficiência, nesta condição de operação, e calcule a potência requerida para acionar a bomba.
Passo 1
Beleza! Vamos começar o exercício aplicando o equilíbrio de energia para o sistema entre o ponto inicial da mangueira (ponto 1) e o ponto final, antes do bocal (ponto 2), dessa forma, temos:
Nesse caso, como a geometria da mangueira é constante, e a vazão deve ser a mesma nos dois pontos, então temos e os termos de velocidade se cancelam. E, como o exercício não mencionou diferença de altura entre os pontos 1 e 2, temos e esses termos também se cancelam: dessa forma a equação se torna:
E, sabemos que a perda de carga, contendo perdas distribuídas e localizadas, pode ser escrita como:
Nesse exercício, não temos perda localizada e nem acessórios com perda de carga com comprimento equivalente associado, então a perda de carga se torna:
Passo 2
Substituindo a equação para a perda de carga na equação de Bernoulli, temos:
E, isolando a velocidade, temos:
Então, como não temos a velocidade e nem o fator de atrito, precisamos recorrer ao diagrama de Moody para estimar um valor para , dessa forma, com:
E, com o diagrama de Moody a seguir:
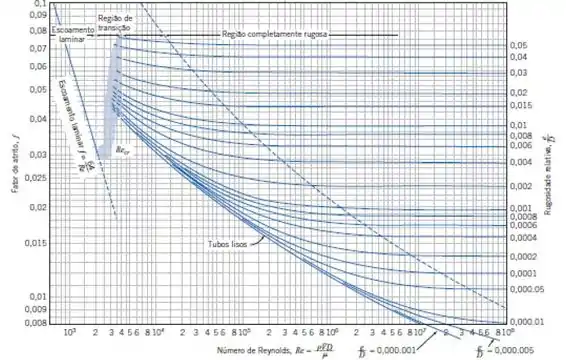
Pegando na região onde temos escoamento totalmente rugoos, que é onde as curvas já estão constantes, temos:
Com esse valor do fator de atrito podemos calcular a velocidade, então:
Lembrando que a variação de pressão equivale à perda de carga ao longo do comprimento da mangueira, então, substituindo os valores conhecidos, temos:
Agora, conferindo se nossa estimativa de foi correta, vamos checar o número de Reynolds para essa velocidade. Então, Reynolds será:
Esse valor de Reynolds já cai na parte totalmente rugosa do escoamento, então nossa estimativa é válida. Então, agora podemos encontrar a vazão de projeto do sistema:
Passo 3
Agora vamos aplicar a equação de Bernoulli para o bocal, entre os pontos de entrada (ponto 1) e de saída (ponto 2), então, temos:
Nesse caso, sabemos que a descarga do bocal ocorre para o ambiente, então temos e faremos para utilizar a pressão manométrica. Sabemos também que é a velocidade encontrada no passo 1 e que é a velocidade de saída do bocal. Nesse caso, podemos desprezar a diferença entre as cotas e , então, a equação se torna:
Substituindo os valores conhecidos, temos:
Passo 4
Para selecionar uma bomba para essa aplicação, precisamos da altura de carga da bomba, que pode ser encontrada através da diferença entre a pressão na entrada do bocal e a pressão com que a água sai do hidrante (lembre-se que devemos considerar a perda de carga, pois a bomba deve fornecer carga suficiente para compensar essa perda também), então, temos:
Substituindo os valores conhecidos, temos:
Para essa altura de carga e para a vazão encontrada no passo 1, com o auxílio do diagrama de seleção de bombas a seguir:
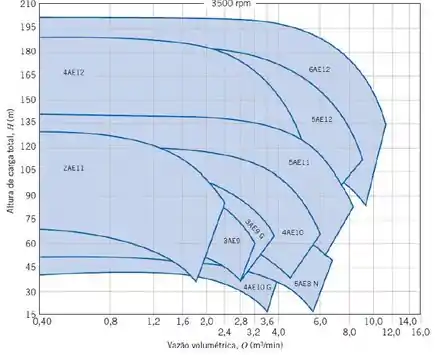
Podemos selecionar a bomba ZAE11 a 3500 rpm.
Passo 5
Agora, para encontrar a eficiência da bomba, vamos nos basear na curva de desempenho da bomba 4AE11, pois não temos curva de desempenho para a ZAE11, então, do gráfico a seguir, temos:
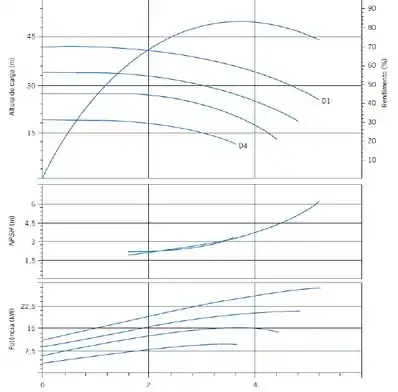
Então, com as condições de operação encontradas, podemos assumir uma eficiência de:
Passo 6
Então, para essa eficiência, a potência para acionar a bomba pode ser encontrada através de:
Substituindo os valores conhecidos, temos: