Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 140

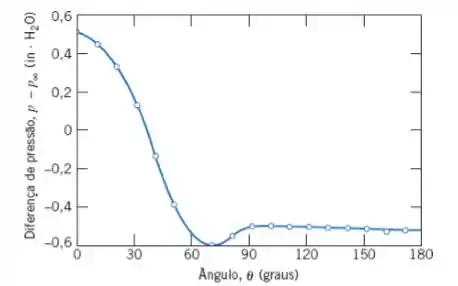
O gráfico mostra diferença de pressão versus ângulo, medido para o escoamento de ar em torno de um cilindro circular para R e = 80.000 . Use estes dados para estimar C A para este escoamento. Compare com os dados da Fig. 9.13. Como você explica a diferença?

Passo 1

Fala aí galera, bora pra mais um problema de Mecânica dos Fluidos. Primeiramente, sabemos que, por definição:

C A = F A 1 2 ρ U 2 A

Desconsiderando os efeitos da viscosidade, temos que, em um elemento infinitesimal:

d F A = d F cos ⁡ θ = p d A c o s θ = p w R d θ cos ⁡ θ

Logo, integrando:

F A = ∫ 0 2 π d F A = ∫ 0 2 π p w R cos ⁡ θ   d θ = 2 ∫ 0 π p w R cos ⁡ θ d θ

No entanto, sabemos que:

∫ 0 π p ∞ cos ⁡ θ d θ = 0

Logo:

F A = ∫ 0 π p - p ∞ cos ⁡ θ w 2 R d θ

A pressão estática é dada por:

p 0 - p ∞ = 1 2 ρ U 2

Portanto:

C A = F D 1 2 ρ U 2 A = ∫ 0 π p - p ∞ cos ⁡ θ w 2 R d θ p 0 - p ∞ ( w 2 R ) = ∫ 0 π p - p ∞ p 0 - p ∞ cos ⁡ θ d θ

Resolvendo a integral:

C A = 1,08

A estimativa da figura 9.13 é de C A = 1,2 .

Esta diferença se dá devido aos efeitos do atrito nas camadas (devido à viscosidade).

Resposta

C A = 1,08

A estimativa da figura 9.13 é de C A = 1,2 .

Esta diferença se dá devido aos efeitos do atrito nas camadas (devido à viscosidade).

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um avião pesa 180 kN e tem uma área de asa de 160 m2 e uma corda média de 4 m. As propriedades de aerofólio são dadas pela Figura 7.25. Se o avião é projetado para pousar a V0 = 1,2 Vestol, usando um
Admita que o avião do Problema 7.116 seja equipado com todos os melhores dispositivos de alta sustentação da Figura 7.28. Qual a sua mínima velocidade de estol em km/h? Calcule a distância de parada s
Na época anterior à guerra, havia uma controvérsia, talvez apócrifa, sobre se o abelhão (também conhecido como mamangaba) teria uma aerodinâmica apropriada para voar. O abelhão B o m b u st e r r e s
Mostre que, se as Equações ( 7.70 ) e ( 7.71 ) são válidas, a razão máxima entre a sustentação e o arrasto ocorre quando C A = 2 C A ∞ . Quais são F S / F A m á x á e a para uma asa simétrica quando R
Em 2001, um avião comercial perdeu toda a potência durante um voo a 10.000m sobre o Oceano Atlântico, a cerca de 100k m da Ilha dos Açores. Os pilotos, com habilidade admirável, colocaram o avião em u