Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 111
Uma bola de tênis de mesa tem massa de 2,6 g e diâmetro de 3,81 cm. A bola será golpeada horizontalmente a uma velocidade inicial de 20 m/s quando estiver a 50 cm acima da mesa, como na Figura P7.111. Para ar ao nível do mar, que rotação (spin), em rpm, fará a bola tocar a extremidade oposta da mesa a 4 m de distância? Faça um cálculo analítico aproximado, usando a Figura P7.108, e leve em conta o fato de que a bola desacelera durante sua trajetória.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos uma bola de beisebol girando a uma velocidade angular desconhecida. Ela parte a uma velocidade inicial .
A bola tem peso e diâmetro e descreve uma trajetória horizontal de
Vamos considerar que essa bola descreve uma seção circular de ângulo e raio , que pode ser enxergada no esquema abaixo que fizemos pra te orientar:
Sendo a velocidade média da bola indo de até o momento que ela cai no chão em .
O enunciado nos pede pra calcular a velocidade angular da bola, e pra isso nós vamos usar suas forças de arrasto e sustentação.
Antes de irmos para os próximos passos, temos que lembrar que as propriedades do ar a temperatura ambiente são e .
Então vem comigo pra gente resolver esse problema juntos!
Passo 2
Vamos então calcular as forças de arrasto e de sustentação com base na velocidade inicial .
Como nos Problemas 7.108 e 7.110, a gente teria que ir no gráfico da figura 7.108. Mas como não temos a velocidade angular, podemos só estimar o coeficiente de arrasto em e deixar a força de sustentação em função de , que iremos descobrir em breve.
Podemos então calcular a desaceleração horizontal será basicamente dada pela força de arrasto, a que age na direção horizontal:
Passo 3
Agora, vamos calcular as propriedades geométricas do arco circular. Pra isso,dê uma olhada na figura exposta no Passo 1. Pra achar e vamos olhar pras seguintes relações trigonométricas:
Resolvendo esse sistema de equações pra e , temos:
Passo 4
Agora, vamos usar pra calcular a velocidade na qual a bola toca o chão, que ocorre a aproximadamente . Sendo assim, sua velocidade final é aproximadamente de .
Portanto, nossa velocidade média será . Com ela e com podemos encontrar a aceleração vertical da bola:
Outra forma de calcular é usando a força de sustentação:
Dessa forma, podemos usar pra calcular o coeficiente de sustentação :
Passo 5
Agora vamos finalizar a questão usando o valor de como valor de entrada na Figura P7.108 pra calcular :
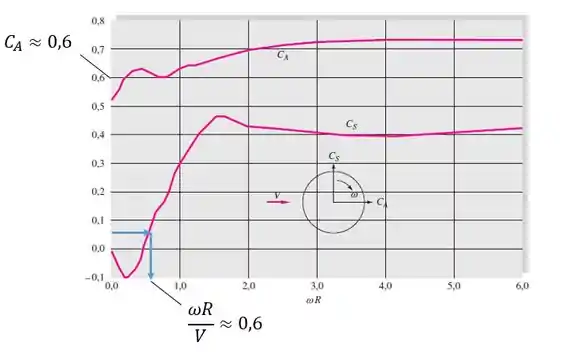
Com o valor de podemos achar o valor da velocidade angular:
Pronto, matamos o problema juntos!
Resposta
A rotação que fará a bola tocar a extremidade da mesa é