Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 112
Uma esfera de madeira (d = 0,65) é ligada por uma barra delgada a uma articulação em um túnel de vento, como na Figura P7.112. Ar a 20ºC e 1 atm escoa e faz a esfera levitar. (a) Plote a variação do ângulo u com o diâmetro d da esfera na faixa 1 cm
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos uma esfera de madeira de massa específica ligada por uma barra de comprimento a uma articulação em um túnel de vento com ar escoando a uma velocidade de , como mostra a figura que ilustra a questão.
A questão quer que a gente plote um gráfico entre o ângulo e o diâmetro da esfera. Nos próximos passos, eu vou te mostrar como encontrar uma expressão relacionando as duas grandezas e como plotar esse gráfico.
Mas antes da gente ir pro Passo 2, vamos lembrar que para o ar à temperatura ambiente, a massa específica será e a viscosidade será .
Agora sim, vem comigo pra gente matar esse problema juntos!
Passo 2
Antes de seguir na resolução, dê uma olhada nesse esquema aí embaixo:
Como vocês podem ver, temos duas forças agindo nesse sistema: a força peso da esfera e a força de arrasto . Elas podem ser calculadas como:
Podemos então fazer um balanço de momento com relação à articulação. Vamos supor o sistema em equilíbrio, ou seja, .
Além disso, sabemos que as distâncias dos pontos de aplicação das forças à articulação devem ser computadas utilizando relações trigonométricas simples.
Dessa maneira, teremos:
Vamos substituir as expressões de e :
Reorganizando e isolando :
Passo 3
Agora vamos responder a letra (a).
Basicamente, o que vamos fazer aqui é calcular os números de Reynolds em função dos diâmetros da esfera e com os valores de Reynolds ir na Figura 7.16 (b), na página 492, e calcular o valor de . Vamos repetir isso pra toda faixa analisada.
O número de Reynolds em função do diâmetro da esfera é dado por:
Vamos analisar essas equações pra esferas de diâmetros de , , e . Pra demostrar os cálculos que vamos fazer, vou te mostrar como fazer pra esfera de .
Primeiro, vamo calcular o Número de Reynolds:
Vamos agora na Figura 7.16 (b):
Ou seja, nesse caso . Vamos agora calcular o valor de :
Repetindo esses passos pros outros valores de diâmetro, podemos traçar o gráfico abaixo:
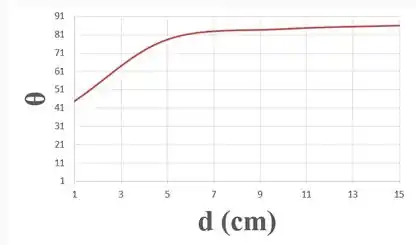
Pronto, matamos a questão juntos!
Resposta
O gráfico plotado é
