Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 7.Problemas - Ex. 88
Uma bomba de água, centrífuga, funcionando à velocidade , tem os seguintes dados para a vazão e altura de carga :
A altura de carga é uma função da vazão, , da velocidade, , do diâmetro do rotor, , e da massa específica da água, . Trace um gráfico da altura de carga em função da vazão. Determine os dois parâmetros para este problema e, a partir dos dados da tabela trace a curva de um parâmetro versus o outro. Usando o Excel, faça uma análise de linha de tendência desta curva e, em seguida, gere e trace um gráfico da altura de carga em função da vazão para velocidades do rotor de 600 rpm e 1200 rpm.
Passo 1
Tá legal, a primeira coisa que devemos fazer é determinar os parâmetros dimensionais, nesse exercício temos:
Então, como temos 5 parâmetros dimensionais, teremos:
Agora vamos escrever a equação dimensional para cada uma das grandezas:
Agora, sabemos que teremos 3 dimensões primárias: , então, temos:
Agora vamos calcular o número de adimensionais independentes , nesse caso temos:
Sendo assim, temos:
Passo 2
Agora vamos construir os números adimensionais:
Agora, substituindo cada uma das grandezas dimensionais nas equações, temos:
Então, para que seja adimensional, temos:
Dessa forma, temos então:
Agora, repetindo o processo para :
Então, para que seja adimensional, temos:
Dessa forma, temos então:
Então podemos escrever em função de :
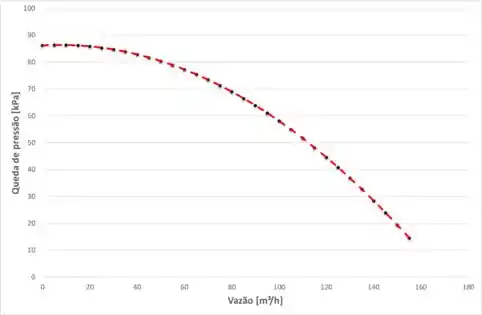
Agora, vamos esboçar o gráfico da relação dada no enunciado entre a vazão e a queda de pressão, então, temos:
Passo 3
Então, a partir do gráfico do passo 2, podemos assumir a relação entre a queda de pressão e a vazão como sendo de segundo grau, dessa forma, a equação que modela o problema terá o formato:
Então, no nosso caso, temos:
Então, escrevendo a queda de pressão e a vazão em função dos adimensionais, os pontos fornecidos no enunciado se tornam:
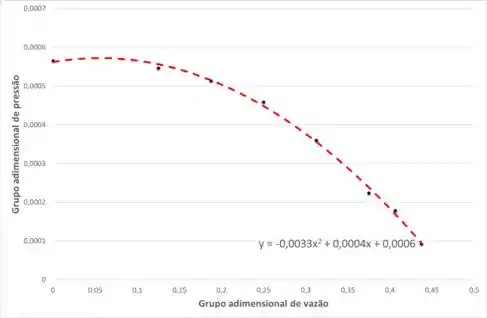
Então, os coeficientes da equação ajustada são:
Então, a equação se torna:
Passo 4
Então, agora podemos plotar o valor para da queda de pressão em função da vazão. Então, teremos:
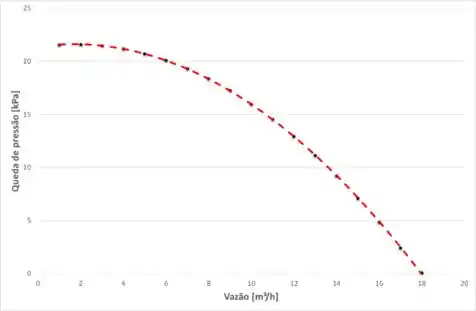
E, agora, para a velocidade , temos:
