Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 54
Considere escoamento laminar completamente desenvolvido em um tubo circular. Use um volume de controle cilíndrico conforme mostrado. Indique as forças que atuam sobre o volume de controle. Usando a equação da quantidade de movimento, desenvola uma expressão para a distribuição de velocidade.
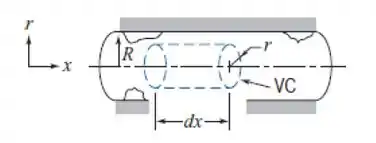
Passo 1
Beleza! Vamos começar desenhando o volume de controle com as forças atuantes sobre ele, então, temos:
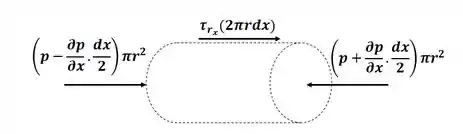
Agora nós vamos escrever a equação do equilíbrio de momento na direção vista no capítulo 4:
No nosso caso, sabemos que não teremos força de campo atuando na direção , então teremos . Sabemos também que, como temos regime permanente, podemos simplificar a derivada no tempo. E, por fim, considerando escoamento totalmente desenvolvido, então podemos simplificar também a integral sobre a superfície de controle, dessa forma, a equação se resume as forças de superfície na direção . Então a equação acima se torna:
Então, simplificando os termos em comum, ficamos com:
Agora, dividindo toda a equação por e agrupando os termos em comum, temos:
Passo 2
No entanto, nós sabemos que podemos escrever a equação para a tensão de cisalhamento como:
Então, igualando essa expressão à expressão obtida no passo 1, temos:
Integrando essa expressão em relação à , temos:
Para descobrir o valor de , vamos aplicar a condição de contorno para , em que , então, temos:
Então, a equação para o perfil de velocidade será: