Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 5.Problemas Abrangentes - Ex. 4

A bomba centrífuga Taco In. modelo 4013 tem um rotor de diâmetro D = 329 mm. Quando bombeia água a 20°C a ômega = 1.160 rpm, a vazão Q medida e o aumento de pressão Dp são dados pelo fabricante da seguinte forma:

(a) Considerando que Dp = f(r, Q, D, omega), use o teorema pi para reescrever essa função em termos de parâmetros adimensionais e depois faça um gráfico com os dados fornecidos na forma adimensional. (b) Deseja-se usar a mesma bomba, girando a 900 rpm, para bombear gasolina a 20°C e 90,85 m3/h. De acordo com a sua relação adimensional, qual é o aumento de pressão Dp esperado em Pa?

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nesse problema, temos que avaliar o aumento de pressão ∆ p   fornecido por uma bomba centrífuga.

A letra (a) nos pede para usar análise dimensional para escrever a função escrever ∆ p   =   f   ( ρ ,   Q ,   D ,   Ω ) como um adimensional.

Além disso, ela nos pede para utilizar uma tabela que demonstra os valores de aumento de pressão em função da vazão volumétrica em L / m i n em rotor de diâmetro D = 329   m m para escrever um gráfico com os parâmetros adimensionais encontrados.

Já a letra (b) nos pede pra usar essa mesma bomba, girando a Ω = 900   r p m para bombear gasolina a 20 ° C e 98,85 m 3 h para descobrir o aumento de pressão ∆ p .

Nos próximos passos eu vou te ajudar a resolver esse problema, então vem comigo!

Passo 2

Em primeiro lugar, iremos resolver a letra (a).

Vamos olhar de novo a função que define o aumento de pressão na bomba:

∆ p   =   f   ( ρ ,   Q ,   D ,   Ω )

Note que nessa função temos n = 5 variáveis e j = 3   dimensões primárias ( M ,   L   , T ). Por análise dimensional, sabemos que isso quer dizer que teremos 2 grupos Pi.

Iremos selecionar ( ρ ,   D ,   Ω ) como as variáveis de repetição, obtendo assim os seguintes parâmetros:

Π 1 = ∆ p ρ Ω ² D ²

Π 2 = Q Ω D ³

Logo, a função de forma adimensionada será:

∆ p ρ Ω ² D ² = f Q Ω D ³

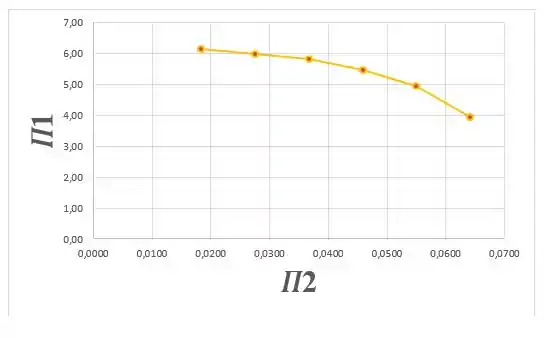
Agora devemos plotar um gráfico de Π 1 em função de Π 2 .

Lembre que temos uma bomba de rotor de diâmetro D = 0 , 329   m , além de Ω = 1160   r p m = 19,33   r p s .

Desta forma, podemos calcular os valores de Π 1 e Π 2 com base nos valores de vazão volumétrica Q e aumento de pressão ∆ p apresentados na Tabela que ilustra o problema.

Como o fluido é água, iremos considerar ρ = 998   k g / m ³ .

A tabela abaixo demonstra os resultados dos cálculos que fizemos para cada uma das vazões volumétricas e incrementos de pressão:

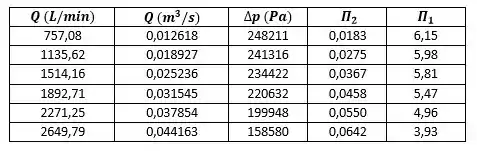
A partir da tabela montada, podemos traçar um gráfico de Π 1 em função de Π 2 :

Passo 3

Pra finalizar a questão, vamo resolver a letra (b).

Utilizando o gráfico que a gente plotou no passo anterior, vamos descobrir o aumento de pressão ∆ p necessário para bombear gasolina a 20 ° C e vazão Q = 98,85 m 3 h = 0,0274 m 3 s , com Ω = 900   r p m = 15   r p s .

Vamos lembrar que para gasolina a 20 ° C temos uma massa específica de ρ = 680   k g / m ³ .

Em primeiro lugar, devemos calcular o valor de Π 2 :

Π 2 = Q Ω D ³ = 0,0274 m 3 s 15   r p s 0,329 ³ = 0,0513

Entrando com esse valor no gráfico, a gente pode descobrir o valor de Π 1 correspondente ao cruzar os dois na curva:

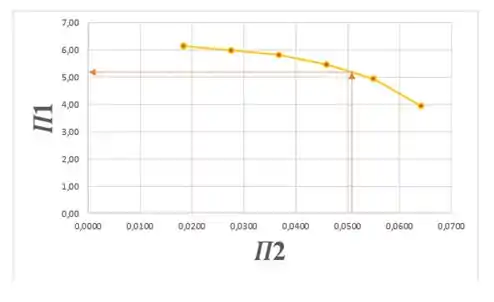
Como é possível notar pela figura, Π 1 ≈ 5,25 .

Pra calcular o valor de ∆ p correspondente basta então fazer:

∆ p ρ Ω ² D ² =   Π 1 →   ∆ p 680 k g m 3 15   r p s 2 0,329 ² =   5,25

∆ p = 86944   P a

Pronto, matamos a questão juntos!

Resposta

(a) A forma adimensional para a função apresentada no enunciado é ∆ p ρ Ω ² D ² = f Q Ω D ³

(b) O aumento de pressão usando a mesma bomba nas especificações indicadas é ∆ p = 86944   P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma correia continua, movendo verticalmente através de um banho de líquido viscoso, arrasta uma camada de líquido de espessura h ao longo dela. Considere que a vazão volumétrica de líquido, Q , depend
No exemplo 5.1 usamos o teorema de pi para desenvolver a equação 5.2 com base na equação 5.1. Em lugar de simplesmente listar as dimensões de cada variável, alguns pesquisadores listam as potências de
A velocidade de propagação C de uma onda capilar em água profunda é conhecida como uma função apenas da massa específica ρ , comprimento de onda λ e da tensão superficial γ . Encontre a relação funcio
A velocidade angular de rotação de um moinho de vento Ω , sem carga, é considerada uma função do diâmetro do moinho D, da velocidade do vento V, da massa específica do ar ρ , da altura do moinho H em
Em condições de escoamento laminar, a vazão volumétrica Q através de um pequeno orifício capilar de seção triangular de lado b e comprimento L é uma função da viscosidade μ , da queda de pressão por u