Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 108
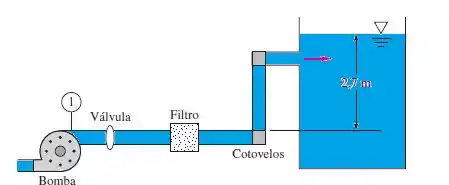
A bomba d’água na figura abaixo mantém uma pressão de 45 kN/m² no ponto 1. Há um filtro, uma válvula de disco aberta pela metade e dois cotovelos normais rosqueados. Há 24 m de tubo de aço comercial de 100 mm de diâmetro. (a) Se a vazão é de 11 L/s, qual é o coeficiente de perda do filtro? (b) Se a válvula de disco é aberta totalmente e , qual a vazão resultante?
Passo 1
E aí, gente!! Tudo bem? Vamos para mais uma aventura com mecflu? Vocês vão sair daqui gostando da matéria, principalmente porque ela é bem aplicável!
Primeira coisa, vamos pegar as propriedades da água, show?
Agora, vamos escrever nossa equação de energia escrita do ponto 1 até a superfície do tanque que está a pressão atmosférica!!
Passo 2
(a) Se liga agora, temos que na superfície, ou seja, no ponto 2, temos que a velocidade é zero e podemos considerar a pressão 2 igual a pressão atmosférica que é MUITO MENOR do que a pressão no ponto 1, então vamos tirar ela da jogada, show?
Passo 3
Agora é trabalho de conta e só! Vamos primeiro calcular nossa velocidade no ponto 1!
Onde é o somatório de todas as perdas de carga menores relacionadas aos acidentes ao longo do trajeto de escoamento.
No livro vamos encontrar os valores de e do cotovelo igual 0,64 e da saída o valor unitário.
Bem, conhecendo a velocidade e o diâmetro, sabemos calcular Reynold e além disso, eu ainda sei também calcular a rugosidade relativa hehe, ou seja, podemos ir no Diagrama de Moody e catar qual seria o nosso valor de f.
A rugosidade do aço comercial é de 0,045 mm, então sua rugosidade relativa é:
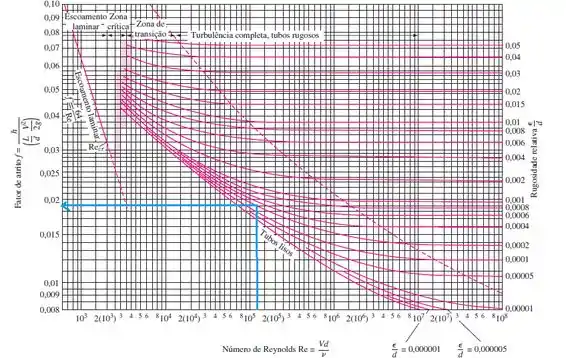
Visualizando no Diagrama de Moddy a gente vê que estamos um pouquinho acima da curva de 0,0004 de rugosidade relativa, então podemos dizer que
Passo 4
Podemos então agora substituir o valor de f na nossa equação, e resolver para o K do filtro
Passo 5
(b) E se Kfiltro = 7 e V for nossa variável desconhecida, o que vamos fazer? Além disso, vamos ter a válvula totalmente aberta, o que nos dá um
Note que temos duas variáveis, e e uma depende da outra, ou melhor, para encontrar f no diagrama de Moody precisamos ter o valor de Reynolds que depende da velocidade.
Então vamos fazer um processo iterativo:
- Chutar o valor de f
- Substituir na equação e calcular V1
- Com o valor de V1, calcular Re
- Com Re e rugosidade relativa, obter o novo valor de f no diagrama de Moddy
- Substituir esse valor na equação para recalcular V1 e dar prosseguimento aos passos seguintes
- O processo será tomado como convergido quando o valor de V1 da iteração anterior for igual ou próximo da iteração seguinte!
Para esse caso, a convergência será tomada quando e, portanto, , o