Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 141

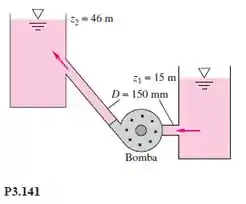
Água a 20 ° C é bombeada a 5.678 L/min de um reservatório inferior para um superior, como na Figura P3.141. As perdas por atrito no tubo são aproximadas por h p   ≈ 27   V ² / ( 2 g ) , em que V é a velocidade média no tubo. Se a bomba tem 75% de eficiência, qual a potência em hp necessária para acioná-la?

Passo 1

Bora pra mais uma!

Primeiramente vamos descobrir a velocidade do fluido:

Q = 5678 L m i n * 1 m 3 1000 l * 1 m i n 60 s = 0,095 m 3 s .

Sendo Q = V * A → V = Q A = Q π * D 2 2 , daí podemos encontrar o valor da velocidade:

V = 0,095 m 3 s π * 0,15 2 m 2 = 5,376 m s .

Agora, vamos jogar o valor da velocidade calculada na equação de perda de carga por atrito enunciada:

h p = 27 * 5,376 m s 2 2 * 9,8 m s 2 = 39,813 m .

Passo 2

O próximo passo será calcular a carga da bomba utilizando a equação da energia. Vamos considerar como ponto 1 a superfície do reservatório mais elevado, e ponto 2 a superfície do reservatório inferior. Daí:

P 1 ρ g + V 1 2 2 g + Z 1 = P 2 ρ g + V 2 2 2 g + Z 2 + h p e r d a - h b o m b a

Mas P 1 = P 2 = P a t m e V 1 = V 2 ≈ 0 . Daí obtemos:

h b o m b a = Z 2 - Z 1 + h p e r d a = 46 m - 15 m + 39,813 m = 70,813 m

Agora, vamos calcular a potência da bomba:

P b o m b a = ρ g Q h b o m b a η b o m b a = 998 k g m 3 * 9,8 m s 2 * 0,095 m 3 s * 70,813 m 0,75 = 87726,88 W = 87,77 3 k W  

Por fim, vamos converter o valor obtido para cavalo vapor:

P b o m b a = 87,773 k W * 1 h p 0,746 k W = 117,6 h p .

Resposta

A potência necessária para acioná-la é de 117,6hp.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Num carburador, a velocidade do ar na garganta do Venturi é 120m / s . O diâmetro da garganta é 25m m . O tubo principal de admissão de gasolina tem um diâmetro de 1,15m m e o reservatório de gasolina
A pressão no ponto S do sifão da figura não deve cair abaixo de 25k P a( a b s ) . Desprezando as perdas, determinar:A velocidade do fluido;A máxima altura do ponto S em relação ao ponto A ; p a t m =
Na extremidade de uma tubulação de diâmetro D , acha-se instalado um bocal que lança um jato de água na atmosfera com diâmetro de 2c m . O manômetro metálico registra uma pressão de 20k P a e a água s
Sabendo que a potência da bomba é 3k W , seu rendimento 75 % e que o escoamento é de 1 para 2 , determinar:A vazão;A carga manométrica da bomba;A pressão do gás.Dados: H p 1,2 = H 5,6 = 1,5m ; H p 3,4
Quais são as vazões de óleo em massa e em peso no tubo convergente da figura, para elevar uma coluna de 20c m de óleo no ponto ( 0 ) ?Dados: desprezar as perdas; γ ó l e o = 8000N / m 3 ó ; g = 10m /