Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 139
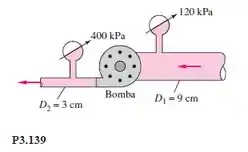
A bomba horizontal da Figura P3.139 descarrega 57 m³/h de água a 20C. Desprezando as perdas, qual é a potência em kW entregue à água pela bomba?
Passo 1
Bora que essa é moleza!!
Vamos primeiro às hipóteses:
- O escoamento ocorre em regime permanente
- O fluido é incompressível
Agora, vamos calcular as velocidades na tubulação anterior a bomba e posterior a ela, note que pela hipótese 1, a vazão mantém-se constante nos dois casos. Daí:
Passo 2
Agora, aplicando a equação da energia, desprezando as perdas conforme o enunciado, temos:
Por fim, vamos calcular a potência da bomba:
Resposta
A potência entregue à água pela bomba é de 83,5kW.
Exercícios de Livros Relacionados
Se a água no tubo do Problema 6.89 está inicialmente em repouso e a pressão do ar é mantida em 21 kPa (manométrica), qual será a aceleração da água no tubo?
Ar comprimido é usado para acelerar a água que sai de um tanque através de um tubo, conforme mostrado. Despreze a velocidade da água no tanque e considere que o escoamento no tubo seja uniforme em qua
Se a água no tubo do Problema 6.89 está inicialmente em repouso e a pressão é mantida em 10,3 kPa (manométrica), deduza uma equação diferencil para a velocidade V no tubo como uma função do tempo, int
Considere o tanque do Problema 4.46. Usando a equação de Bernoulli para escoamente não permanente ao longo de uma linha de corrente, avalie a mínima razão entre diâmetros, D / d , necessária para just
Esboce cuidadosamente as linhas de energia (LE) e as linhas piezométricas (LP) para o sistema mostrado na Fig. 6.6, se uma bomba (adicionando energia ao fluido) estiver localizada no ponto 2, ou no po