Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 92
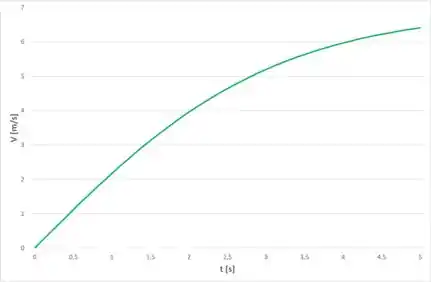
Se a água no tubo do Problema 6.89 está inicialmente em repouso e a pressão é mantida em 10,3 kPa (manométrica), deduza uma equação diferencil para a velocidade no tubo como uma função do tempo, integre e trace um gráfico de em função de , para a .
Passo 1
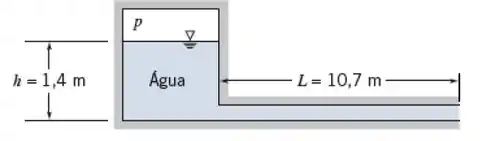
Tá legal, vamos começar o exercício aplicando a equação de Bernoulli para regime transiente entre o reservatório (ponto 1) e a saída do tubo (ponto 2), então, temos:
Nesse caso, como o ponto 2 está exposto à atmosfera, temos , dessa forma, iremos obter uma pressão manométrica. Sabemos também que dentro do reservatório, podemos considerar . Dessa forma, a equação se torna:
Conforme vimos no Problema 6.89, a velocidade não depende do trajeto entre 1 e 2, então, podemos retirar esse termo da integral e reescrevê-lo como uma derivada simples, então a equação de Bernoulli se torna:
Passo 2
Como o caminho é simplesmente o comprimento , a equação de Bernoulli se torna:
Agora separando as variáveis, temos:
Integrando essa expressão dos dois lados, temos:
Com o auxílio de uma calculadora, chegamos em:
Passo 3
Plotando o gráfico da função obtida no passo 2, temos:
