Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 90
Se a água no tubo do Problema 6.89 está inicialmente em repouso e a pressão do ar é mantida em 21 kPa (manométrica), qual será a aceleração da água no tubo?
Passo 1
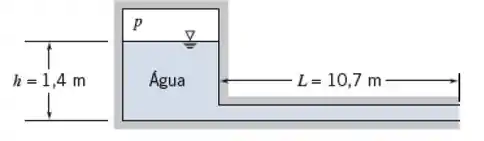
Tá legal, vamos começar o exercício aplicando a equação de Bernoulli para regime transiente entre o reservatório (ponto 1) e a saída do tubo (ponto 2), então, temos:
Nesse caso, como o ponto 2 está exposto à atmosfera, temos , dessa forma, iremos obter uma pressão manométrica. Sabemos também que dentro do reservatório, podemos considerar e o enunciado nos disse que a água no tubo está inicialmente em repouso, então . Dessa forma, a equação se torna:
Conforme vimos no Problema 6.89, a velocidade não depende do trajeto entre 1 e 2, então, podemos retirar esse termo da integral e reescrevê-lo como uma derivada simples, então a equação de Bernoulli se torna:
Passo 2
Como o caminho é simplesmente o comprimento , a equação de Bernoulli se torna:
No entanto, nós sabemos que a aceleração é a derivada da velocidade no tempo, ou seja:
Então, reescrevendo a equação de Bernoulli, temos:
Então, substituindo os valores conhecidos, temos a pressão no interior do tanque para o instante dado: