Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas - Ex. 71

A bomba do Problema 11.38, operando a 3.500   r p m , fornece água a 20 ° C através de 2.195   m   ( 7200   f t ) de tubo horizontal de aço comercial de 125   m m   0,417   f t de diâmetro. Há uma entrada e uma saída em canto vivo, quatro cotovelos de 90 ° e uma válvula gaveta. Calcule (a) a vazão, se a válvula estiver totalmente aberta, e (b) o percentual de fechamento da válvula que faz a bomba operar no PMR. (c) Se essa última condição permanecer continuamente por 1 ano, calcule o custo da energia a R $   0,25 por k W h .

Passo 1

E aí, prontos para resolvermos mais uma questão juntos?

Bora lá!

Começamos o nosso problema obtendo as seguintes propriedades da água a 20 ° C da Tabela A.1:

ρ = 1,94   s l u g / f t 3

μ = 2,09 × 10 - 5   s l u g / f t ⋅ s

Devemos obter o PMR a partir dos dados fornecidos:

P M R = 350   g a l / m i n

Todos os coeficientes de perda para cotovelos e uma válvula de gaveta aberta são obtidos da Tabela 6.5:

K c o t = 0,28

K v a l = 0,1

Já os coeficientes de perda de entrada e saída são obtidos na Figura 6.21:

K e n t = 0,5

K s a i = 1

Calculando o coeficiente de perda total:

∑ K = 4 K c o t + K v a l + K e n t + K s a i

∑ K = 4 ⋅ 0,28 + 0,1 + 0,5 + 1

∑ K = 2,72

Passo 2

Letra a)

Escrevendo a expressão para a altura de carga do sistema:

H = V 2 2 g f L d + ∑ K

H = Q π 4 d 2 2 2 g f L d + ∑ K

Presumindo:

f = 0,017

Substituindo os dados:

  H = Q π 4 ⋅ 0,41 6 2 2 2 ⋅ 32,2 ⋅ 0,017 ⋅ 7200 0,41 6 + 2,72

H = 204,3 Q 2

Tabelando os dados fornecidos e traçando um gráfico para obter a equação da curva da bomba:

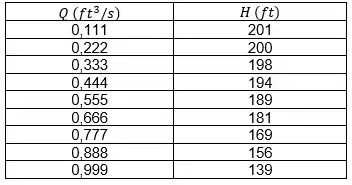
Plotando o gráfico:

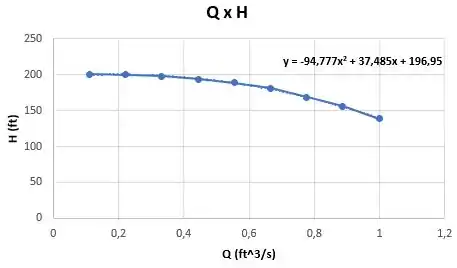
A partir do gráfico, obtemos a seguinte equação da curva da bomba:

H = - 94,777 Q 2 + 37,485 Q + 196,95

Igualando a altura de carga da bomba e do sistema:

H s = H b

204,3 Q 2 = - 94,777 Q 2 + 37,485 Q + 196,95

Resolvendo a equação:

Q = 0,8765   f t 3 / s

Passo 3

Calculando a velocidade da água:

V = 4 Q π d 2

Substituindo os dados:

V = 4 ⋅ 0,8765 π ⋅ 0,416 2

V = 6,43   f t / s

Calculando o número de Reynolds:

R e = ρ V d μ

R e = 1,94 ⋅ 6,43 ⋅ 0,416 2,09 × 10 - 5

R e = 2,48 × 10 5

Obtendo o fator de rugosidade para tubo de aço comercial na Tabela 6.1:

ε = 0,00015   f t

Calculando a relação de rugosidade:

ε d = 0,00015 0,417 = 0,00036

Pelo Diagrama de Moody, com R e = 2,48 × 10 5 e ε d = 0,00036 , obtemos:

f = 0,0178

Passo 4

Substituindo os dados na equação de altura de carga do sistema:

H s i s t = Q π 4 d 2 2 2 g f L d + ∑ K

H s i s t = Q π 4 ⋅ 0,416 2 2 2 ⋅ 32,2 ⋅ 0,0178 ⋅ 7200 0,416 + 2,72

H s i s t = 259,15 Q 2

Igualando H s i s t com H b o m b :

259,15 Q 2 = - 94,777 Q 2 + 37,485 Q + 196,95

Q = 0,8008   f t 3 / s

Calculando a velocidade da água:

V = 4 Q π d 2

Substituindo os dados:

V = 4 ⋅ 0,8008 π ⋅ 0,416 2

V = 5,872   f t / s

Calculando o número de Reynolds:

R e = ρ V d μ

R e = 1,94 ⋅ 5,872 ⋅ 0,416 2,09 × 10 - 5

R e = 2,271 × 10 5

Obtendo o fator de atrito novamente pelo Diagrama de Moody, para R e = 2,271 × 10 5 e ε d = 0,00036 :

f = 0,0175

Então, nossa premissa é válida.

Portanto

Portanto, nossa premissa é próxima ao valor obtido.

Portanto, a taxa de fluxo se a válvula estiver totalmente aberta é de 0,8008   f t 3 / s

Passo 5

Letra b)

Equilibrando a altura de carga da bomba e do sistema:

H s i s t = H b o m b

X Q 2 = - 94,777 Q 2 + 37,485 Q + 196,95

Substituindo Q :

X ⋅ 0,8008 2 = - 94,777 ⋅ 0,8008 2 + 37,485 ⋅ 0,8008 + 196,95

X = 286,1

Substituindo os dados na equação de H s i s t :

H s i s t = Q π 4 ⋅ 0,416 2 2 2 ⋅ 32,2 ⋅ 0,0178 ⋅ 7200 0,416 + 2,62 + K v a l

Assim:

286,1 ⋅ Q 2 = Q π 4 ⋅ 0,416 2 2 2 ⋅ 32,2 ⋅ 0,0178 ⋅ 7200 0,416 + 2,62 + K v a l

286,1 ⋅ Q 2 = Q 2 1,19 ⋅ 310,204 + K v a l

K v a l = 30

Portanto, a válvula deve estar  30 % aberta.

Passo 6

Letra c)

Calculando o nível de potência no PMR:

P = ρ Q g H n

Substituindo os dados, com n = 0,81 :

P = 1,94 ⋅ 0 , 777 ⋅ 32,2 ⋅ 169 0,81

P = 13,6   k W

Calculando o custo anual:

C = 13,6 ⋅ 365 ⋅ 24 ⋅ 0,1

C = $ 11904

E assim a gente termina a nossa questão!

Até a próxima!

Resposta

a )   0,8008   f t 3 / s

b )   30 %

c )   C = $ 11904  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um grupo de engenheiros está projetando uma nova turbina-hidráulica, escalando uma turbina existente. A turbina existente (turbina A ) tem diâmetro D A = 1,50m e gira a n ˙ A = 150r p m . No seu ponto
Uma bomba centrífuga de 292 mm de diâmetro, operando a 1.750 rpm, fornece 3,22 m3/min e uma altura de carga de 32 m no ponto de melhor rendimento (82%). (a) Essa bomba pode operar eficientemente quand
Um soprador para folhas é essencialmente um rotor centrífugo cuja saída vai para um tubo. Suponha que o tubo seja de PVC liso, com 1,2 m de comprimento e diâmetro de 63 mm. A velocidade de saída desej
PA11.1 – A altura de carga de uma bomba para aquário pequena é dada pelo fabricante como uma função da vazão volumétrica, listada a seguir:Qual é a vazão máxima que pode ser atingida se você utiliza e
PA11.3 – Reconsidere o Problema P6.77 como um exercício de seleção de turbinas. Selecione um tamanho e uma rotação de rotor da família de turbinas Francis da Figura 11.22d para fornecer uma potência m