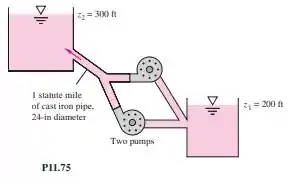
Duas bombas de da Figura 11.7b são associadas em paralelo para o sistema da Figura P11.75. Despreze as perdas localizadas. Para água a calcule a vazão e a potência necessária se (a) ambas as bombas estiverem funcionando e (b) uma bomba for desligada e isolada.
Passo 1
Fala galera, beleza?
Bora resolver essa questão juntos!
Então, vem comigo!
Começamos o nosso problema obtendo as propriedades da água, a , a partir da tebela de propriedades da água:
Calculando a velocidade no tubo:
Com:
Substituindo os dados na nossa equação:
Passo 2
Letra a)
Na Fig. 11.7 (b), para um tubo de 35 pol. de diâmetro, temos a seguinte equação para altura de carga da bomba:
Quando ambas as bombas estão funcionando, a taxa de fluxo em cada tubo é , substituindo na nossa equação:
Obtendo a equação da altura de carga do sistema aplicando a equação de energia:
Com:
Substituindo os dados:
Obtendo o fator de rugosidade para ferro fundido:
Assim, temos que o valor de rugosidade relativa é dado por:
Devemos supor que o fluxo seja turbulento, obtendo o fator de atrito do Diagrama de Moody:
Substituindo na nossa equação:
No ponto “ótimo” de operação, a altura de carga da bomba e do sistema devem se coincidir em um ponto. Assim:
Passo 3
Calculando a vazão de cada bomba:
Da Fig. 11.7 (b) para de diâmetro de tubo e taxa de fluxo de , temos uma eficiência correspondente de .
Calculando a altura de carga manométrica da bomba substituindo :
Calculando a potência total necessária para operar ambas as bombas usando a seguinte equação:
Passo 4
Letra b)
Na Fig. 11.7 (b), para um tubo de 35 pol. de diâmetro, temos a seguinte equação para altura de carga da bomba:
Obtendo a equação da altura de carga do sistema aplicando a equação de energia:
Com:
Obtendo o fator de rugosidade para ferro fundido:
Assim, temos que o valor de rugosidade relativa é dado por:
Devemos supor que o fluxo seja turbulento, obtendo o fator de atrito do Diagrama de Moody:
Substituindo na nossa equação:
No ponto “ótimo” de operação, a altura de carga da bomba e do sistema devem se coincidir em um ponto. Assim:
Passo 5
Da Fig. 11.7 (b) para de diâmetro de tubo e taxa de fluxo de , temos uma eficiência correspondente de .
Calculando a altura de carga manométrica da bomba substituindo :
Calculando a potência total necessária para operar ambas as bombas usando a seguinte equação:
E fim!
Te espero na próxima questão!