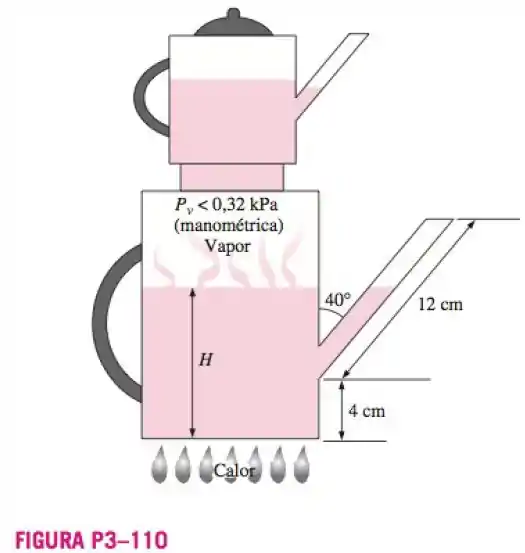
Um bule de chá com infusor na parte superior é usado para fazer chá, como mostra a Figura . O infusor pode impedir parcialmente que o vapor escape, fazendo com que a pressão no bule suba e ocorra um transbordamento do tubo de serviço, Desprezando a expansão térmica e a variação na quantidade de água do tubo de serviço com a relação à quantidade de água do bule, determine o peso máximo da água fria que não causaria um transbordamento a pressões manométricas de até para o vapor.

Utilizando as considerações anteriores, primeiramente temos que determinar a altura total da coluna de água que podemos ter, seria , este que pode ser determinado por trigonometria.

Temos o seguinte, triangulo retângulo:

Tendo nosso .

Após isto, para determinarmos a coluna de água máxima que podemos colocar seria o seguinte:

Temos e agora vamos determinar , variação está que é dada a partir da pressão manométrica no bule, após isto poderemos calcular o volume máximo de água e com o volume máximo utilizando a formula da densidade da água poderemos determinar a quantidade de peso máximo.

Agora que temos as colunas que faltavam, para podermos determinar q coluna máxima de e água que pode ser despejada no bule.

Calculando o volume:

Temos que a massa para este volume seria:

E o peso para esta massa seria:

Bem pessoal, creio que está seria uma saída para resolução do problema, mas o enunciado do livro não nos deu informações suficientes para resolver o problema, caso ele desejasse e peso de água máximo para que não transbordasse o bule.