Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 8
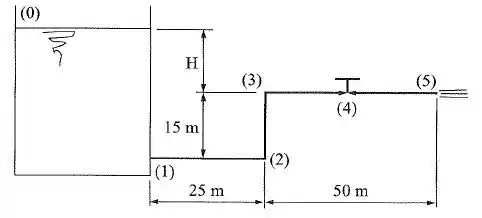
Calcular a vazão na tubulação da figura para . Calcular em seguida o novo valor de para que a vazão seja . Dados: ; ; ;
Passo 1
Vamos começar o exercício aplicando o equilíbrio de energia entre os pontos 0 e 5:
Sabemos que podemos escrever a perda de carga como a soma da perda distribuída mais as perdas localizadas da seguinte forma:
Substituindo essa relação na equação de cima, junto com os valores já conhecidos, temos:
Nesse caso, como a vazão no sistema é constante e o diâmetro da tubulação também, então temos , dessa forma, podemos isolar da equação anterior:
Passo 2
Como não temos o valor de , devemos recorrer ao diagrama de Moody a seguir, para isso precisamos encontrar o valor de , nesse caso, como temos uma seção circular, então , nesse caso, temos:
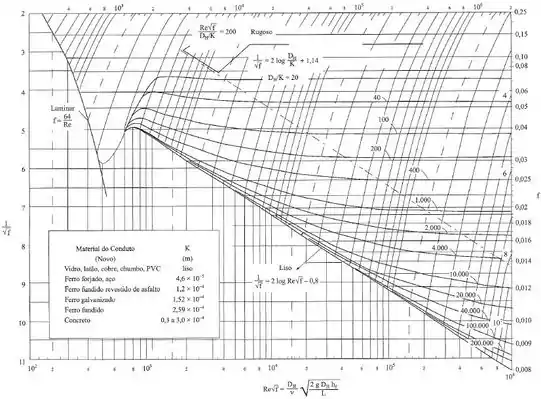
Lembrando que sempre supomos um valor na parte do diagrama onde o escoamento é rugoso, que é a parcela onde as curvas possuem um valor constante (ocorrem para altos valores de ), dessa forma, para a relação encontrada, vamos adotar:
Agora podemos retornar a equação da velocidade obtida no passo 1 e substituir os valores conhecidos:
Agora devemos verificar o número de Reynolds para ver se nosso palpite a respeito de foi coerente, então, calculando Reynolds:
Então, para esse valor de Reynolds, podemos ver no diagrama de Moody que a já se encontra constante, então nossa suposição foi válida. Então agora podemos calcular o valor da vazão para o sistema:
Passo 3
Agora vamos calcular o valor da altura , para uma vazão de 50 L/s, então, para essa vazão, a nova velocidade será:
Agora, se aplicarmos novamente o equilíbrio de energia entre os pontos 0 e 5, vamos obter a mesma equação obtida no passo 1:
Só que agora estamos interessados em obter o valor de , que nada mais é do que o pedido no enunciado, então, substituindo os valores conhecidos nessa equação, temos: