Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 87
Na entrada de um trecho de diâmetro constante da tubulação do Alasca, a pressão é 8,5 MPa e a elevação é 45 m; na saída, a elevação é de 115 m. A perda de carga nessa seção da tubulação é 6,9 kJ/kg. Calcule a pressão na saída.
Passo 1
Considerando a Figura a seguir, este problema buscará obter a pressão na saída (seção 2).
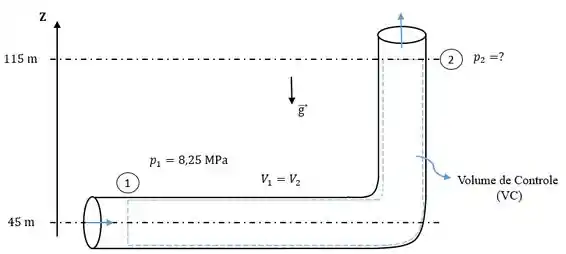
Para obter tal parâmetro será utilizada a Equação de Energia, em kJ/kg, aplicada entre as seções 1 e 2, conforme expressão:
Para a aplicação da equação apresentada, as seguintes hipóteses são necessárias:
- regime permanente ();
- escoamento incompressível ();
- Não houve especificação do fluido em escoamento, então considerando trata-se do óleo SAE 10W, então ;
- diâmetro constante, logo .
- em ambas as seções de avaliação;
- ;
- ;
- ;
Passo 2
Tendo como objetivo a pressão , ela pode ser escrita como:
Sabendo que :
Passo 3
Utilizando os parâmetros conhecidos:
Assim, a pressão na saída é: