Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 4

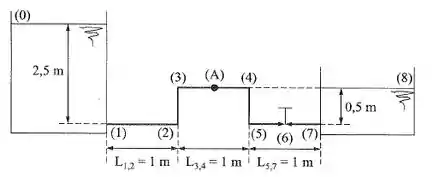
Dada a instalação da figura, determinar:

a) a velocidade e a vazão na tubulação;

b) a pressão no ponto A, ponto médio do trecho (3)-(4).

Dados: k s 1 = 0,5 ; k s 2 = k s 3 = k s 4 = k s 5 = 1 ; k s 6 = 10 ; k s 7 = 1 ; D = 6   c m ; k = 0,15   c m ; g = 10   m / s 2 ; ν = 10 - 6   m 2 / s ; γ = 10 4   N / m 3 .

Passo 1

Vamos começar esse exercício aplicando o equilíbrio de energia entre os pontos 0 e 8:

H 0 = H 8 + H p 0,8

v 0 2 2 g + p 0 γ + z 0 = v 8 2 2 g + p 8 γ + z 8 + H p 0,8

Substituindo os valores conhecidos:

0 2 2 g + 0 γ + 2,5 = 0 2 2 g + 0 γ + 0,5 + H p 0,8 → H p 0,8 = 2   m

Agora, sabemos que a perda de carga no sistema é a soma da perda distribuída h f mais as perdas localizadas h s , então, podemos escrever a perda de carga como:

H p 0,8 = h f + ∑ h s → H p 0,8 = f L v 2 2 g D H + v 2 2 g ∑ k s

Agora vamos isolar v da equação:

H p 0,8 = v 2 2 g f L D H + ∑ k s → v 2 = 2 g H p 0,8 f L D H + ∑ k s → v = 2 g H p 0,8 f L D H + ∑ k s

Passo 2

Nesse caso, como temos v em função de f e as duas variáveis desconhecidas, vamos ter que recorrer ao diagrama de Moody a seguir e adotar um valor de f , então, para isso precisamos encontrar o valor de D H / k , nesse caso, como temos uma seção circular, então D H = D = 6.10 - 2   m

D H k = 6.10 - 2 0,15.10 - 2 → D H k = 40

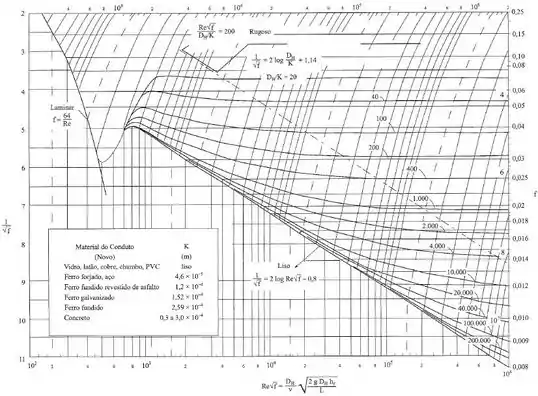
Para esse valor, e pegando um ponto considerando Reynolds alto o suficiente para que a curva seja constante e já tenha atingido o estado de escoamento rugoso, então teremos:

f = 0,054

Agora, substituindo esse valor na equação para a velocidade encontrada no passo anterior, temos:

v = 2 g H p 0,8 f L D H + ∑ k s = 2 10 2 0,054 4 6.10 - 2 + 0,5 + 1 + 1 + 1 + 1 + 10 + 1

v = 1,45   m / s

Agora precisamos ver se adotamos um f coerente, para isso vamos calcular Reynolds:

R e = v D ν = 1,45 0,06 10 - 6 → R e = 8,7.10 4

E, conforme podemos ver no gráfico, para esse valor de Reynolds, a curva já possui comportamento constante.

Então podemos calcular a vazão do sistema:

Q = v A = v π D 2 4 = 1,45 π 0,06 2 4 → Q = 4,1.10 - 3   m 3 / s

Passo 3

Agora para encontrar a pressão no ponto A, vamos aplicar o equilíbrio de carga entre os pontos 0 e A:

H 0 = H A + H p 0 , A

v 0 2 2 g + p 0 γ + z 0 = v A 2 2 g + p A γ + z A + H p 0 , A

Substituindo os valores conhecidos:

0 2 2 g + 0 γ + 2,5 = v 2 2 g + p A γ + 0,5 + H p 0 , A → p A γ = 2 - v 2 2 g - H p 0 , A

Conforme vimos no passo 1, podemos escrever a perda de carga como (só lembrar agora que o comprimento L é o comprimento só até o ponto A e a perda de carga localizada da mesma forma, só até o ponto A):

H p 0 , A = h f + ∑ h s → H p 0 , A = f L v 2 2 g D H + v 2 2 g ∑ k s

Substituindo esse valor na equação anterior:

p A γ = 2 - v 2 2 g - f L v 2 2 g D H - v 2 2 g ∑ k s

Substituindo os valores conhecidos, temos:

p A γ = 2 - 1,45 2 2 10 - 0,054 2,0 1,45 2 2 10 0,06 - 1,45 2 2 10 0,5 + 1 + 1 → p A γ = 1,4 5

p A = 1,4 5 10 4 → p A = 14 , 5   k P a

Resposta

v = 1,45   m / s

Q = 4,1.10 - 3   m 3 / s

p A = 14 , 5   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A instalação da figura será utilizada para o transporte de 12 L/s de água do reservatório A para o reservatório C, ambos mantidos em nível constante. A bomba será adquirida do fabricante X, que produz
Na instalação da figura, a água deve ser lançada por meio de um bocal no tanque da direita. Determinar a mínima potência da bomba para que isso aconteça. Dados: D = 10c m ; material: ferro fundido; di
Considere um tubo de ferro galvanizado, horizontal, de 5 cm de diâmetro. Qual deve ser a mínima queda de pressão da água, num trecho de 30 m de comprimento, para que o escoamento seja turbulento e hid
Na instalação da figura, determinar a potência da bomba necessária para produzir uma vazão de 10 L/s, supondo seu rendimento de 70%. Dados: D r e c = 2,5 " ( 6,25c m ) ; D s u c = 4 " ( 10c m ) ; aço;
Um conduto de ferro fundido de 1000 m de comprimento e 10 cm de diâmetro liga dois reservatórios em níveis constantes, e foi projetado para uma vazão de 20 L/s de água. Colocada em funcionamento a ins