Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 73

Gate AB is 5 ft wide into the paper and opens to let fresh

water out when the ocean tide is dropping. The hinge at A

is 2 ft above the freshwater level. At what ocean level h

will the gate fi rst open? Neglect the gate weight.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

Os dados são os seguintes:

Comprimento do portão: A B = 5   f t

Altura da dobradiça pra água do mar: 2 f t

Nível do oceano: h

O desenho é o seguinte

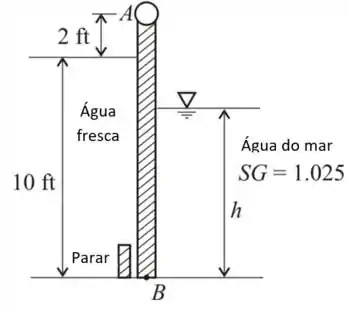
Passo 2

Lado da água doce:

Área de água doce exposta ao portão = 10 × 5 = 50 f t 2 Altura do centro de gravidade: h C G = 5 f t Peso específico da água: γ w = 62.4 l b f / f t 3 Força hidrostática que atua sobre o portão

F w = γ w A h   = 62.4 × 50 × 5   = 15600 l b f

Linha de ação da força hidrostática:

γ C p = - I n n A h C G

y c p = 1 12 × 5 × 10 3 50 × 5   = - 5 3   = 1.6667

Passo 3

Lado da água do mar:

Área da água do mar exposta ao portão = 5 × h = 5 h   m 2 Altura do centro de gravidade: h C G = h 2 f t

Peso específico da água do mar γ mar   = S G × γ w

  = 1.025 × 62.4   = 63.96 l b f / f t 3

Força hidrostática que atua sobre o portão

F S = γ mar   × A mar   × h C G   = 63.96 × 5 h × h 2   = 159.9 h 2 l b f

Linha de ação da força hidrostática no lado da água do mar

y c = I x x A ⋅ h C G   = 1 12 × 5 × h 3 5 h × h 2   = - h 6

Passo 4

O diagrama de corpo livre é o seguinte

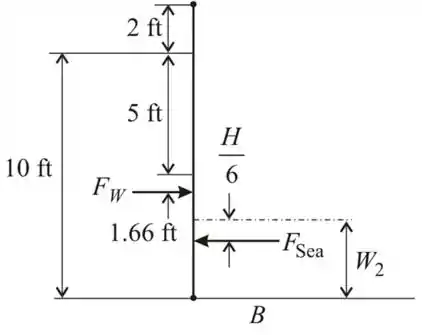
Passo 5

O momento sobre dobradiça A :

  ∑   M A = F w ( 5 + 2 + 1.6667 ) - F S 10 + 2 - h 2 - h 6   = F w ( 8.6667 ) - F S 12 - h 3

Quando o portão tende a abrir, o momento torna-se zero em A :

  ∑   M A = 0 F w ( 8.6667 ) - F S 12 - h 3 = 0 F w × 8.6667 = F S 3 ( 36 - h ) 15600 × 8.6667 = 159.9 h 2 3 ( 36 - h ) h 3 - 36 h 2 + 2536.5951 = 0 h = 9.848

O portão será aberto em h = 9.848 f t

Resposta

h = 9.848 f t

Exercícios de Livros Relacionados

Repita o problema P2.77 para deduzir uma expressão analítica para P em função e h. Há alguma coisa incomum na sua solução?
Na figura abaixo, a comporta AB fecha uma abertura circular de 80 cm de diâmetro. A comporta é mantida fechada por uma massa de 200 kg como mostrado. Suponha a gravidade padrão a 20°C. Em que nível h
A comporta circular ABC na figura abaixo tem um raio de 1 m e é articulada em B. Calcule a força P exatamente suficiente para impedir que a comporta se abra quando h = 8 m. Despreze a pressão atmosfér
Na figura abaixo a comporta AB tem 3 m e largura e está conectada por um cabo e polia a uma esfera de concreto (d = 2,4). Qual é o menor diâmetro da esfera suficiente para manter a comporta fechada?
A comporta AB da figura abaixo é articulada em A, tem a largura b e estabelece um contato suave em B. A comporta tem massa específica ρ s e espessura uniforme t. Para qual massa específica ρ s da comp