Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 84

Panel AB in Fig. P2.84 is a parabola with its maximum at

point A. It is 150 cm wide into the paper. Neglect atmospheric pressure. Find (a) the vertical and (b) the horizontal

water forces on the panel.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

O diagrama abaixo mostra o painel A B tendo uma forma de parábola

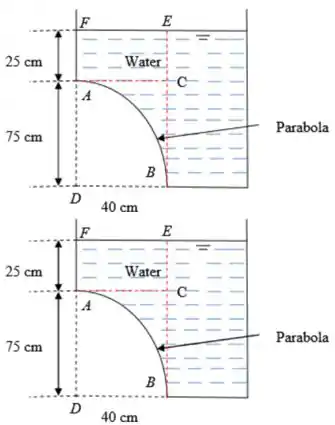
Passo 2

(a) A força vertical é a força de peso exercida pela água acima da parábola. É calculado somando o peso do retângulo e o peso A C E F da curva cercada por A B C (vermelho pontilhado). O peso da porção retangular é,

F v 1 = γ á g u a   V 1 … … ( 1 )

Aqui, V 1 é o volume de retângulo A C E F , e γ á g u a   é o peso específico da água.

Passo 3

Calcule o volume do retângulo A C E F com uma largura de 150   c m .

V 1     = 25 × 40 × 150       = 150000   c m 3 × 1   m 100   c m 3       = 0.15   m 3  

Substitua os valores de 9790   N / m 3 para γ á g u a   e 0.15   m 3 para V 1 na equação (1).

F v y 1     = 9790 × 0.15       = 1468.5   N  

Passo 4

O peso da parte curvilínea A B C é,

F v 2 = γ á g u a   V 2 … …   ( 2 )  

Aqui o volume do caminho curvilíneo A B C é V 2 .

A área delimitada pela parábola A B é 2 / 3 de área delimitada pelo retângulo A C B D . A área restante acima da parábola A B é 1 / 3 de área delimitada pelo retângulo A C B D .

Portanto, o volume do caminho curvilíneo A B C é 1 / 3 de volume delimitado pelo retângulo A C B D .

Passo 5

Calcule o volume delimitado pelo ângulo reto A C B D .

V A C B D     = 750 × 40 × 150       = 450000   c m 3 × 1   m 100   c m 3       = 0.45   m 3  

O volume do caminho curvilíneo A B C é,

V 2     = 1 3 V A C B D       = 1 3 × 0.45       = 0.15   m 3  

Passo 6

Substitua 9790   N / m 3 por γ á g u a   , e 0.15   m 3 por V 2 na equação (2).

F v 2     = 9790 × 0.15       = 1468.5   N  

Calcule a força vertical total conforme mostrado abaixo:

F v     = F v 1 + F v 2       = 1468.5 + 1468.5       = 2937   N  

Portanto, a força hidrostática vertical no painel é 2937   N .

Passo 7

(b) A força horizontal no painel é calculada pela projeção vertical do painel.

F H = P C G A p r o j e t a d a  

Aqui, é a P C G pressão no centroide e h C G é a distância da superfície para o centroide do painel. Calcule a pressão no centroide usando a expressão abaixo:

P C G = γ á g u a   h C G

Passo 8

Calcule h C G .

h C G     = 25 + 75 2       = 62.5   c m × 1   m 100   c m       = 0.625   m  

Substitua 9790   N / m 3 por γ á g u a e 0.625   m para h C G .

P C G     = γ á g u a   h C G       = 9790 × 0.625       = 6118.75   P a  

Passo 9

Calcule a área vertical projetada do painel.

A p r o j e t a d a       = 75 × 150       = 11250   c m 2 × 1   m 100   c m 2       = 1.125   m 2  

Substitua 6118.75   P a por P C G , e 1.125   m 2 por A p r o j e t a d a   na equação (3).

F H     = 6118.75 × 1.125       = 6883.6   N  

Portanto, a força hidrostática horizontal no painel é 6883.6   N .

Resposta

a) F v = 2937   N

b) F H = 6883.6   N

Exercícios de Livros Relacionados

Na figura abaixo, a comporta AB tem 1,5 m de largura e o limitador B irá quebrar se a força da água for igual a 41000 N. Para qual profundidade de água essa condição é alcançada?
Na figura abaixo, a força hidrostática F é a mesma no fundo dos três recipientes, apesar de os pesos dos líquidos acima serem muito diferentes. As três formas dos fundos e os fluidos são iguais. Isso
A comporta AB na figura abaixo tem 1,2 m de comprimento e 0,8 m de largura. Desprezando a pressão atmosférica, calcule a força F na comporta e a posição X de seu centro de pressão.
A comporta AB na figura abaixo tem 1,5 m de largura, está articulada em A e limitada por um limitador em B. A água está a 20°C. Calcule (a) a força no limitador B e (b) as reações em A se a profundida
O exemplo 2.5 calculou a força na placa AB e sua linha de ação, usando a abordagem de momento de inércia. Alguns professores dizem que é mais instrutivo calcular esses valores por integração direta da