Gate AB in Fig. P2.83 is a quarter circle 10 ft wide into the
paper and hinged at B. Find the force F just sufficient to
keep the gate from opening. The gate is uniform and
weighs 3000 lbf.
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
Desenhando a configuração do portão
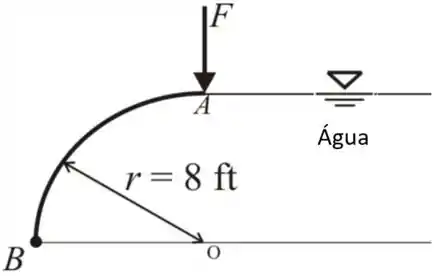
Passo 2
Calcule o componente horizontal da força hidrostática como se fosse vertical.
Aqui, é o peso específico da água e é a posição do centroide da área projetada a partir da superfície da água. Substitua por por , e por .
Passo 3
Calcule o momento de inércia do plano .
Encontre a posição em que a força horizontal atua.
Aqui, é a posição em que age a partir do ponto . Substitua por por , e por .
Passo 4
Calcule o componente vertical da força hidrostática. O componente vertical da força hidrostática é igual ao peso do pedaço de água que falta acima do portão.
Substitua por por por e por
Passo 5
As figuras abaixo mostram a localização da força vertical
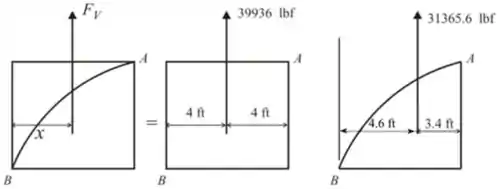
Passo 6
Encontre a posição em que a força vertical atua considerando a soma dos momentos da figura acima em . O momento resultante é igual ao momento criado pela força vertical em .
O peso da porta atua no centroide do quarto de círculo em a partir do ponto , ou a partir do ponto Substitua para .
Desenhe o diagrama de corpo livre do portão.
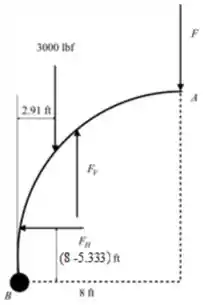
Passo 7
Considere o momento sobre .
Portanto, a força suficiente para impedir que o portão se abra é .