Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 92
Cálculos preliminares para uma usina hidrelétrica mostram que uma altura de carga líquida de 715 m está disponível com uma vazão de água de 2m³/s. Compare a geometria e a eficiência de rodas Pelton projetadas para funcionar a (a) 450 rpm e (b) 600 rpm.
Passo 1
Tá legal! Precisamos primeiro pegar alguns dados da Figura 10.11 apresentada nessa seção, como a eficiência máxima para o sistema de rodas Pelton e a sua velocidade específica correspondente, então, temos:
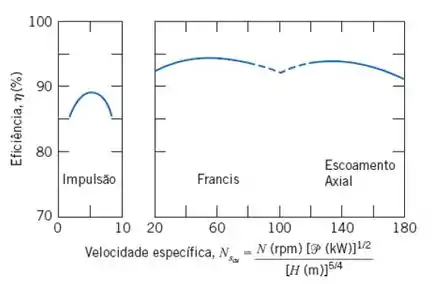
Dessa forma, como as rodas Pelton são classificadas como máquinas de impulsão, a eficiência máxima será:
E, para esse valor, temos uma velocidade específica de:
Agora, sabemos que a potência de saída do sistema pode ser escrita como:
Então, substituindo os valores conhecidos, temos:
Passo 2
Agora, vamos analisar a turbina para o caso da letra a), onde temos . Só que antes disso, ao fazer as contas com as unidades sugeridas abaixo do gráfico fornecido no livro, obtemos:
Esse valor fica fora da faixa utilizada, então a escala do gráfico fornecido não corresponde ao cálculo da velocidade específica com essas unidades, então vamos utilizar as unidades do sistema inglês, onde temos em rpm, em hp e em pés, então, convertendo as informações, temos:
E a equação para a velocidade específica se torna:
Agora sim caímos na faixa de estudo, e para esse valor de velocidade específica temos uma eficiência correspondente de:
Passo 3
Então agora vamos encontrar a velocidade do jato ainda para o caso da letra a):
Agora precisamos encontrar a velocidade da roda, que será dada pela figura 10.36 junto com a eficiência de 0,88 encontrada, então, temos:
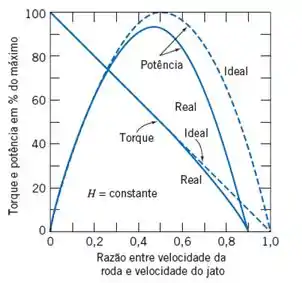
Então, para a eficiência de 0,88, temos uma razão de:
Então, o diâmetro da roda pode ser encontrado através da equação:
E o raio pode ser encontrado através da velocidade da roda:
Então o diâmetro da roda será:
Agora podemos encontrar o diâmetro do jato através da equação da vazão, onde temos:
Substituindo os valores conhecidos, temos:
E, por fim, a relação entre o diâmetro do jato e da roda será:
Passo 4
Agora, vamos analisar a turbina para o caso da letra b), onde temos . E a equação para a velocidade específica se torna (lembrando de usar os dados do sistema americano):
Agora sim caímos na faixa de estudo, e para esse valor de velocidade específica temos uma eficiência correspondente de:
Note que esse valor é o que consideramos para a eficiência máxima.
Passo 5
Então agora vamos encontrar a velocidade do jato para o caso da letra b):
Agora precisamos encontrar a velocidade da roda, que será dada pela figura 10.36 junto com a eficiência de 0,89 encontrada, então, temos:
Então, para a eficiência de 0,88, temos uma razão de:
Então, o diâmetro da roda pode ser encontrado através da equação:
E o raio pode ser encontrado através da velocidade da roda:
Então o diâmetro da roda será:
Agora podemos encontrar o diâmetro do jato através da equação da vazão, onde temos:
Substituindo os valores conhecidos, temos:
E, por fim, a relação entre o diâmetro do jato e da roda será: