Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 4.Problemas - Ex. 43
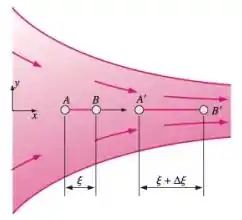
O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Como o escoamento é simétrico com relação ao eixo , o segmento de reta ao longo do eixo permanece no eixo, mas se estica do comprimento até o comprimento ao escoar ao longo do eixo central do canal (Figura P4-43). Gere uma expressão analítica para a variação do comprimento do segmento de reta . (Sugestão: Use os resultados do Problema 4-41.)
Passo 1
Vamos começar definindo as hipóteses do problema:
- O escoamento está em regime permanente;
- O escoamento é bidimensional.
Vamos usar a equação deduzida no Problema 4-42. A posição da partícula em um tempo arbitrário é:
Passo 2
Para a partícula A no tempo , sua localização é dada por:
Para a partícula B:
Como e , podemos escrever uma expressão para como:
Resposta
Exercícios de Livros Relacionados
Um elemento de fluido bidimensional de dimensões d x e d y é transladado e distorcido como mostra a Figura P 4 - 60 durante o período de tempo infinitesimal d t = t 2 - t 1 . As componentes da velocid
Considere um campo de escoamento em regime permanente, bidimensional e incompressível no plano x y . A taxa de deformação linear na direção x é de 2,5s - 1 . Calcule a taxa de deformação linear na dir
Um elemento de fluido bidimensional de dimensões d x e d y é transladado e distorcido como mostra a Figura P 4 - 60 durante o período de tempo infinitesimal d t = t 2 - t 1 . As componentes da velocid
Explique a relação entre vorticidade e rotacionalidade.
Um tanque cilíndrico de água gira em rotação de corpo rígido, no sentido anti-horário com relação a seu eixo vertical (Figura P 4 - 64 ) com velocidade angular ω = 360r p m . Calcule a vorticidade das