Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 2.Problemas - Ex. 33
Em uma camada plana de carvão, com espessura , ocorre geração volumétrica uniforme a uma taxa devido à lenta oxidação de partículas de carvão. Com base em valores médios diários, a superfície superior da cama da transfere calor por convecção para o ar ambiente, no qual e , enquanto recebe irradiação solar em uma quantidade . Irradiação a partir da atmosfera pode ser desprezada. A absortividade em relação aos raios solares e a emissividade da superfície são, cada uma, .
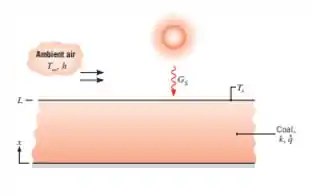
(a) Escreva a forma para o regime estacionário da equação da difusão térmica para a camada de carvão. Verifique se essa equação é satisfeita pela distribuição de temperaturas com a forma
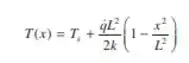
A partir dessa distribuição, o que você pode dizer sobre as condições existentes na superfície inferior ? Esboce a distribuição de temperaturas e aponte suas principais características.
(b) Obtenha uma expressão para a taxa de transferência de calor por condução, por unidade de área, em . Aplicando um balanço de energia em uma superfície de controle ao redor da superfície superior da camada, obtenha uma expressão para . Calcule e para as condições especificadas.
Passo 1
E aí, beleza?
Fica de olho para não se perder e vem comigo resolver essa questão!
Letra a)
Começamos o nosso problema a partir da seguinte equação:
Substituindo a seguinte equação dada:
Temos:
Integrando:
Rearranjando:
Ou seja, todos os valores de satisfazem a equação!
Continuando, devemos esboçar o gráfico do comportamento da temperatura em função de :
Integrando:
Assim, quando , .
O nosso gráfico tem a seguinte forma:
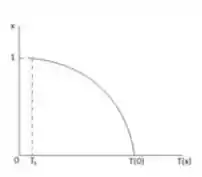
Passo 2
Letra b)
Partindo do balanço de energia, temos:
Abrindo a nossa equação:
Isolando :
Substituindo os dados:
Resolvendo essa equação:
Passo 3
Por último:
Substituindo os dados:
Uffa!
Até a próxima questão!
Resposta
Todos os valores de satisfazem a nossa equação.