Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 103

Rejeitos radioativos são colocados em um recipiente esférico de parede delgada. Os rejeitos geram energia térmica de forma não uniforme de acordo com a relação q ˙ = q ˙ e [ 1 - ( r / r e ) ² ] , na qual q ˙ é a taxa local de geração de energia por unidade de volume, q ˙ e é uma constante e r e é o raio do recipiente. Condições de regime estacionário são mantidas pela imersão do recipiente em um líquido que se encontra a T ∞ e fornece um coeficiente convectivo h uniforme.

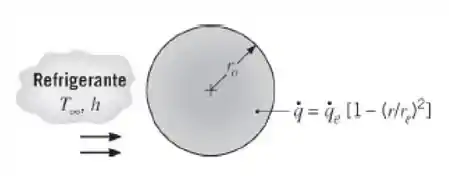
Determine a distribuição de temperaturas, T(r), no interior do recipiente. Expresse o seu resultado em termos de q ˙ e , r e , T ∞ , h e da condutividade térmica k dos rejeitos radioativos.

Passo 1

Beleza! A primeira coisa que vamos fazer é escrever a equação da difusão para sistemas radiais com geração, então, temos:

1 r 2 . d d r k r 2 . d T d r + q ˙ = 0 → d d r r 2 . d T d r = - q ˙ r 2 k

Só que, nos foi dada a expressão para q ˙ , então, substituindo a expressão dada na equação acima, ficamos com:

d d r r 2 . d T d r = - q ˙ e r 2 k 1 - r r e 2 → d d r r 2 . d T d r = - q ˙ e k r 2 - r 4 r e 2

Agora vamos integrar essa expressão em r , dessa forma, iremos obter:

r 2 . d T d r = - q ˙ e k r 3 3 - r 5 5 r e 2 + C 1 → d T d r = - q ˙ e k r 3 - r 3 5 r e 2 + C 1 r 2

Agora, integrando novamente, chegamos em:

T r = - q ˙ e k r 2 6 - r 4 20 r e 2 - C 1 r + C 2

Passo 2

Agora precisamos descobrir o valor das constantes C 1 e C 2 . Para isso, vamos primeiro utilizar a condição de contorno de que não temos fluxo de calor em r = 0 , então, podemos escrever:

r = 0 → d T d r = 0

Substituindo esses valores na expressão obtida no passo 1, chegamos em:

d T d r = - q ˙ e k r 3 - r 3 5 r e 2 + C 1 r 2 → 0 = - q ˙ e k 0 3 - 0 3 5 r e 2 + C 1 0 2 → C 1 = 0

E, nossa segunda condição de contorno será que, na extremidade em r = r e , a transferência de calor por condução será igual àquela por convecção, então podemos escrever:

- k d T d r r = r e = h T r e - T ∞

Substituindo as expressões conhecidas, temos:

- k - q ˙ e k r e 3 - r e 3 5 r e 2 = h - q ˙ e k r e 2 6 - r e 4 20 r e 2 + C 2 - T ∞

q ˙ e r e 3 - r e 5 = h - q ˙ e k r e 2 6 - r e 2 20 + C 2 - T ∞

2 q ˙ e r e 15 h = - 7 q ˙ e r e 2 60 + C 2 - T ∞ → C 2 = 2 q ˙ e r e 15 h + 7 q ˙ e r e 2 60 + T ∞

Então, a equação para o perfil de temperatura será:

T r = - q ˙ e k r 2 6 - r 4 20 r e 2 - C 1 r + C 2

T r = - q ˙ e k r 2 6 - r 4 20 r e 2 + 2 q ˙ e r e 15 h + 7 q ˙ e r e 2 60 + T ∞

Resposta

T r = - q ˙ e k r 2 6 - r 4 20 r e 2 + 2 q ˙ e r e 15 h + 7 q ˙ e r e 2 60 + T ∞

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja a placa plana do Problema 3.112, porém com os sumidouros de calor a temperaturas diferentes, T ( 0 )=T e e T ( L )=T L , e com a superfície inferior não mais isolada termicamente. Agora pode ocor
Seja a pilha de células a combustível do Problema 1.58. As membranas com espessura t = 0,42 mm têm uma condutividade térmica nominal de k=0,79 W m K , que pode ser aumentada para k e f , x=15,1 W m K
Um nanotubo de carbono está suspenso atravessando uma vala de largura s = 5 mm que separa duas ilhas, cada uma a T ∞ = 300K . Um feixe laser irradia o nanotubo, a uma distância ξ da ilha esquerda, for
Um bastão muito longo, com 5 mm de diâmetro e condutividade térmica uniforme k = 25 W m K , é submetido a um processo de tratamento térmico. Sua porção central, com 30 mm de comprimento, está envolta
Um bastão de metal de comprimento 2L, diâmetro D e condutividade térmica k está encravado em uma parede de um isolante perfeito, expondo a metade do seu comprimento a uma corrente de ar que se encontr