Considere a parede plana, o cilindro longo e a esfera mostrados esquematicamente, todos com o mesmo comprimento característico a, mesma condutividade térmica k e mesma taxa volumétrica de geração de energia uniforme .
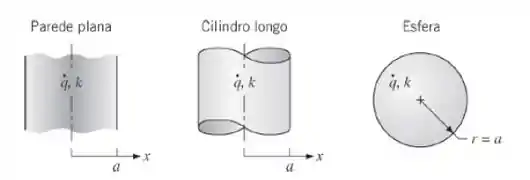
(a) No mesmo gráfico, represente a temperatura adimensional em regime estacionário, , em função dos comprimentos característicos adimensionais, x/a ou r/a, para cada geometria.
(b) Que geometria tem a menor diferença de temperaturas entre o centro e a superfície? Explique esse comportamento comparando a razão volume/área superficial.
(c) Que geometria seria preferível para uso como um elemento combustível nuclear? Explique por quê.
Passo 1
Tá legal! Para começar a letra (a) vamos consultar o apêndice C do livro e buscar as equações para cada uma das geometrias representadas. Então, para a parede plana, temos a equação C.22, dessa forma:
Nesse caso, precisamos deixar a equação no formato pedido no enunciado, nesse caso, temos , então, podemos escrever:
Agora, vamos pegar a equação C.23 para o bastão cilíndrico:
Nesse caso temos , então, reescrevendo a equação, temos:
Passo 2
E, agora, para a esfera, temos a equação C.24:
Nesse caso nós temos . Escrevendo a equação no formato de interesse, chegamos em:
Agora nós vamos representar as equações encontradas em um gráfico em função do valor adimensional e , então, temos:
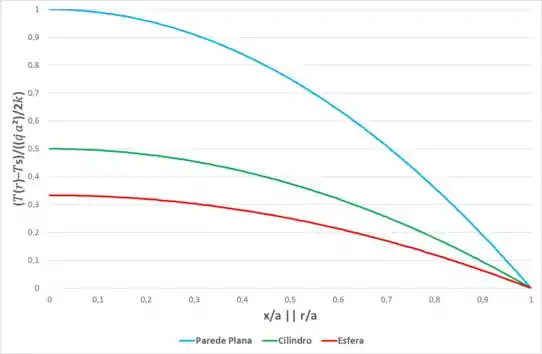
Passo 3
Agora, para a letra (b), nós temos que comparar a relação entre volume e área superficial para cada uma das geometrias. Então, começando pela parede plana, temos:
Agora, para o cilindro temos:
E, por fim, para a esfera, temos:
Como podemos ver, a menor relação entre o volume e a área superficial é a da esfera, então ela terá a menor diferença de temperatura entre o seu centro e a superfície. Podemos comprovar isso olhando para o gráfico encontrado no passo 2.
Passo 4
Por fim, para a letra (c), temos que para o uso de um elemento combustível nuclear, o ideal seria utilizar uma esfera, pois temos uma menor diferença de temperatura entre seu centro e a superfície, e com isso é mais fácil controlar a geração e transferência de calor.