Rejeitos radioativos ( = 20 W/(m · K)) são armazenados em um recipiente esférico de aço inoxidável ( = 15 W/(m · K)), com raios interno e externo iguais a = 0,5 m e = 0,6 m. Calor é gerado no interior dos rejeitos a uma taxa volumétrica uniforme e a superfície externa do recipiente está exposta a um escoamento de água no qual h = 1000 W/(m² · K) e = 25°C.

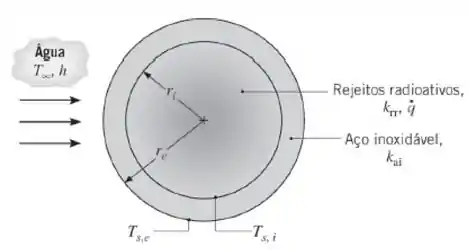
(a) Calcule a temperatura da superfície externa , em condições de regime estacionário.

(b) Calcule a temperatura da superfície interna , em condições de regime estacionário.

(c) Obtenha uma expressão para a distribuição de temperaturas, T(r), nos rejeitos radioativos. Expresse o seu resultado em termos de , , e . Calcule a temperatura em r = 0.

(d) Uma extensão proposta para o projeto anterior envolve o armazenamento de rejeitos radioativos com a mesma condutividade térmica e duas vezes a taxa de geração de calor () em um recipiente de aço inoxidável com raio interno equivalente ( = 0,5 m). Considerações de segurança ditam que a temperatura máxima do sistema não deve exceder 475°C e que a espessura da parede do recipiente não deve ser inferior a t = 0,04 m, sendo preferencialmente igual ou próxima à do projeto original (t = 0,1 m). Avalie o efeito da variação do coeficiente convectivo externo até o valor máximo atingível de h = 5000 W/(m² · K) (através do aumento da velocidade da água), e da espessura da parede do recipiente. A extensão proposta é factível? Caso afirmativo, recomende condições operacionais e de projeto apropriadas para h e t, respectivamente.

Agora, para a letra (b), nós vamos aplicar um equilíbrio de energia somente na superfície do recipiente, onde o calor trocado por condução saindo do recipiente é igual ao calor por convecção trocado com a água, então podemos escrever:

Podemos escrever o calor de condução em função da resistência térmica de condução, que é dada por:

Dessa forma, o calor de condução pode ser escrito como:

Então podemos escrever os calores como:

Substituindo os valores conhecidos, temos:

Agora, para a letra (c), nós vamos escrever a equação da difusão de calor para o sistema radial, então, temos:

Integrando essa expressão em dos dois lados, obtemos:

Integrando novamente essa expressão em , obtemos:

Agora, para descobrir o valor das constantes, vamos aplicar as condições de contorno. Temos que no centro do recipiente, não há fluxo de calor, então:

Substituindo esses valores na equação obtida para , chegamos em:

Para nossa outra condição de contorno, vamos utilizar a temperatura da superfície interna encontrada no passo 2. Então, temos:

Substituindo esses valores na expressão para a temperatura, temos:

Então, a equação para o perfil de temperatura será:

E, então, em , temos:

Agora, para a letra (d), nós iremos utilizar o conceito de resistência térmica. Então, a resistência total do sistema será a resistência por condução mais a resistência por convecção, então, teremos:

Agora, sabemos que pela resistência térmica, podemos escrever:

Então, para cada e , obtendo o valor de dessa equação, e depois substituindo na equação para o perfil de temperatura encontrado no passo 3 em . Conseguimos obter a seguinte relação entre os coeficientes de convecção e as temperaturas no interior dos rejeitos radioativos:

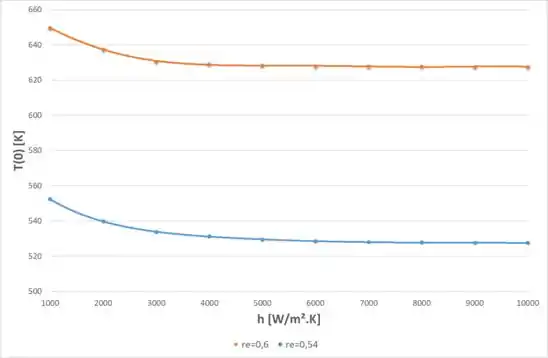
Então, como podemos ver, nem para o melhor caso, que seria com e conseguimos manter a temperatura menor do que 475 °C, e como podemos ver, o incremento em não altera significativamente o valor da temperatura no centro.