Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 1
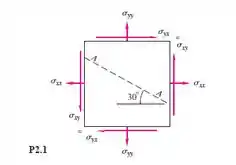
Para o campo de tensão bidimensional da Figura P2.1 sabe-se que
Encontre as tensões de cisalhamento e normal (em ) que atuam sobre o plano de corte AA no elemento a um ângulo de 30° como mostra a figura.
Passo 1
Vamo lá resolver essa questão!
No corte AA, vamos ter o seguinte esquema para entender melhor a questão.
Teremos que, para encontrar as tensões de cisalhamento e a normal no corte AA utilizaremos o somatório de forças, assim:
Calculando cada força separada, vamos começar pela normal, que aponta para fora, assim:
Substituindo os valores dados, teremos:
Passo 2
Para encontrar a tensão de cisalhamento, tangencial a superfície, usaremos o mesmo raciocínio, assim:
Substituindo os valores dados, teremos:
Resposta
Exercícios de Livros Relacionados
Umcampodevelocidadeédadopor V → = a x 3 i + b x y 3 j , em que a = 1 m - 2 s - 1 ,b = 1 m - 3 s - 1 . Determine a equação das linhas de corrente para qualquer tempo t . Trace diversas linhas de corren
Paraoscamposdevelocidadedadosabaixo,determine: a.Seocampodeescoamentoéuni,bioutridimensional,eporquê. b.Seoescoamentoéemregimepermanenteoutransiente,eporquê.(Asquantidadesaeb sãoconstantes.) 1 v → = a
Ocampodevelocidadeédadopor V → = a x i - b t y j , em que a = 1 s - 1 ,b = 1 s - 2 . Determine a equação das linhas de corrente para qualquer tempo t . Trace diversas linhas de corrente no primeiro qu
A velocidade para um escoamento permanente incompressível no plano x y é dada por v → = i ^A / x+ j ^A / x 2 , em que A=2m 2 / s e as coordenadas são medidas em metros. Obtenha uma equação para a linh
Considere o campo de escoamento V → =a x ti ^+bj ^ , em que a=0,1s - 2 e b=4m / s . As coordenadas são medidas em metros. Para a partícula que passa pelo ponto ( x ,y )=( 3 ,1 ) no instante t=0 , trac